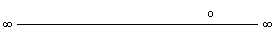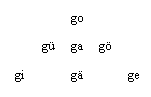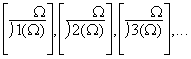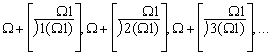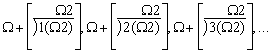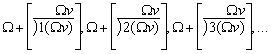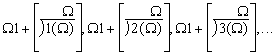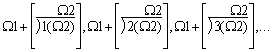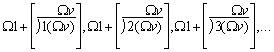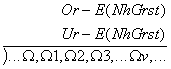Menschliches und digitalisiertes Bewusstsein

Das Unendliche und die Grenze

Peter Paul Sarnig

1 Die menschliche Intelligenz

Wir möchten anstelle des üblichen Begriffes der künstlichen Intelligenz (KI) den der digitalisierten Intelligenz (DI) verwenden, worunter wir in Hardware abwickelbare, digitalisierte Pro­gramme verstehen, die menschliche Erkenntnis­operationen im wei­testen Sinne (1.2) kopieren oder simulieren. Die Summe der menschlichen Erkennt­nisoperationen (1.2) bezeichnen wir als menschliche In­telligenz (MI).

Natürlich besteht schon dadurch ein untrennbarer Zusammenhang zwischen MI und DI, als DI immer ein Teil der schöpferischen, innovativen Seite der MI ist. Einer der Väter der DI gab zu, dass er an die Konstruktion von Rechnern ging, um sich die lä­stige Rechenarbeit als Ingenieur zu erleichtern. Es ist auch mit Sicherheit anzunehmen, dass die Schachgroßmeister, wenn die Computer sie ernstlich bedrängen, die Qualität des Schachspieles auf die nächste Stufe brin­gen werden, indem sie selbst mit Hilfe von Computern spielen. (Derzeit ist dies bereits für den überwiegenden Teil der Weltelite der Fall. Die nächste Stufe wird sein, dass Schachgroßmeister Schach-Computerpro­gramme erstellen.)

Bei Sichtung der bisherigen Diskussion zum Thema, inwieweit DI in der Lage ist, sein wird oder grundsätzlich sein kann, MI abbildgleich zu simulieren oder zu erset­zen, fällt als Erstes auf, dass der Streit zwei Seiten hat.

Zum einen werden auf der Seite der DI die technischen Möglichkeiten und Grenzen im Hard- und Softwarebereich diskutiert und mit Erscheinungen der MI in Verbindung gebracht. Die andere Seite, der hier vor allem unser Augenmerk gelten wird, setzt sich in wechselvoller Weise mit der Frage auseinander, wo eigentlich die Grenzen der MI liegen. Hierbei gelangen die verschiedenen Theoretiker, sowohl die Gegner als auch die euphorischen Vertreter der Möglichkeiten der DI, zu äußerst unter­schiedlichen Ergebnissen. Mit anderen Worten: Das men­schliche Erkenntnis­vermögen, die Erkennt­nisoperationen werden selbst unterschiedlich interpre­tiert und theoretisch erfasst, und es gibt eine Vielzahl von Theorien darüber, wo wir die Grenzen der menschli­chen Erkenntnisoperationen zu ziehen haben. Je nach diesen Grenz­ziehungsverfahren kann man die Theorien über die MI als MI(1), MI(2) usw. be­zeichnen. Kurz: Die Theoretiker bauen ver­schieden enge oder weite Zäune, innerhalb welcher die MI erkennen darf, soll oder muss. Die ver­schiedenen Zäune sind die un­terschiedlichen Erkenntnistheo­rien.

Nun besteht natürlich eine Beziehung zwischen den verschiedenen Grenzen, die man der MI zuweist, und den Möglichkei­ten, diese MI in DI zu simulieren.

Je en­ger die Grenze für die Erkenntnisoperationen der MI gezogen wird, je begrenzter MI formuliert wird, umso eher kann man an­nehmen, sie durch DI simulierbar zu machen. Man ist häufig überrascht über die engen Ansätze hinsichtlich der Fähigkeiten der MI, die im Felde der Diskus­sion benützt werden. Sind die Grenzen der MI aber zu eng gezogen, was derzeit in fast allen Erkenntnis­theorien geschieht, so schadet dies nicht nur dem Wissenschaftsbetrieb und damit der Gesellschaft gene­rell, weil da­durch die Ge­fängnisse vergrößert werden, in denen die Menschen leben müssen. Es schadet auch der Beziehung der MI zur DI und der Entwicklung der letzteren. Werden nämlich die Kerker, die man schon der MI baut, noch durch diejenigen der DI erweitert, so sind damit die Entwicklungsvorausset­zungen von Kunst und Wis­senschaft schwer gehemmt.

1.1    Grenzen der MI = Erkenntnis der menschlichen Erkenntnis

Der Leser wird vielleicht schon merken, wie wichtig es für un­seren Problem­kreis ist, die menschlichen Erkenntnisfähigkeiten genau zu analysieren. Das heißt aber eigentlich nichts anderes, als sich die gesamte Geschichte der Philo­sophie auf diesem Planeten vor Augen zu führen und zu sehen, welch unterschiedliche Antworten auf diese Frage bisher gegeben wurden. Wie weit oder wie eng wurden da die Grenzen gezogen? Wie haben sich trotz Änderung der Wortkleider der Theorien die Grundfra­gen erhalten? Hier können und wollen wir diese Entwicklung nicht darstellen. Wohl aber möchten wir nicht verhehlen, dass wir in den folgen­den Ausführungen über die Fähigkeiten der MI für die Zukunft richtungsweisende neue Gedanken vorbrin­gen, die eigentlich alle bisherigen Erkenntnistheorien der Geschichte vervollstän­digen und eine neue Grundlage der Logik und Mathematik ent­halten. Dieses neue Fundament, das ich "MI(o)" – der Index "o" nicht als "Null", sondern als Buchstabe "o" – nennen möchte und das in Rücksicht auf den Leser nur in vereinfachten For­men und Strukturen dargestellt wird, reicht aber aus, sichtbar zu machen, dass die Grenzen der MI anders zu ziehen sind, als dies bisher geschah. Es fallen bestimmte Mauern, Fesseln wer­den gelöst, ohne dass die bisherigen Erkenntnistheorien negiert oder bekämpft werden. Sie bilden teilirrige, zu enge oder ein­seitige Sonderfälle. [Alle MI(1), MI(2) usw. sind in/unter MI(o) enthalten.] Der Unterschied dieser Studie zu den bisherigen Abhandlungen zum Thema besteht vor allem in Folgendem: a)     Die Grenzen der MI werden neu und weiter gezogen als bisher, womit auch Mathematik und Logik sowie Wissen­schaft und Kunst neue Grundlagen erhalten; die bisherige erkenntnistheoretische Bemühung um Auffindung einer Grund­struktur von Begriffen für ein adäquates wissenschaftliches Denken (Denkkategorien) und einer entsprechenden Logik und Mathematik wird als legi­tim anerkannt. Die Mängel in den bisherigen Erkenntnistheorien, formalen und inhaltlich bestimmten Logiken und der Mathematik werden aufgezeigt. b)     Aus den Neuerungen in a) ergeben sich völlig neue Aspekte hinsichtlich der Grenzen der DI, da die unendlichen Grundlagen der neuen Grundbegriffe und Grund"sätze" (Axiome) der Erkenntnistheorie, Logik und Mathematik und deren logisch-mathematische Beziehun­gen nicht digitalisierbar sind.

1.2    Gliederung, Struktur der menschlichen Erkenntnisoperationen

Die folgenden Ausführungen werden sicher manchem Leser ungewohnt sein. Mögen sie wenigstens dazu beitragen, ihm sichtbar zu machen, um welche Probleme es eigentlich geht, wenn man beginnt, die Erkenntnis des menschlichen Erkennt­nisvermögens und der Erkenntnisoperationen zu untersuchen.  

 

 

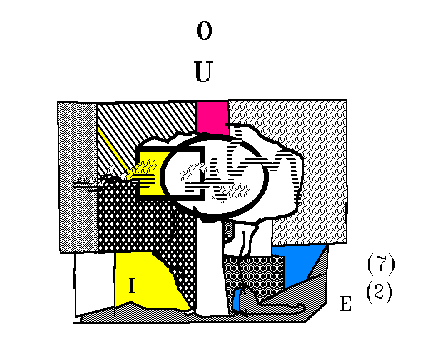
Wir benützen die FIGUR 1. Ein Mensch erkennt die Welt außer sich, Natur G (Landschaft, Bäume usw.) und die Gesellschaft G(1) um sich, also z. B. seine Familie, die deutsche Sprache, die Zeilen, die er hier liest. Eine Außenwelt, Natur G und eine Ge­sellschaft G(1), erkennen wir nicht unmittelbar. Zugänglich sind uns von ihr nur Zustände unserer Sinnesorgane des Körpers E (blau) – vgl. unter 1.2.1 –, die wir her­einnehmen in die Phantasie D (grün). Durch die nach­bildende äußere Phantasie D(1) und die schöpferische, innere Phantasie D(2) und mit Be­griffen C (gelb), die wir teilweise bereits bei der Geburt in un­serem "Bewusstsein" besitzen (C1), teils aus dem Gesellschaftssystem G(1) übernehmen, in welches wir hineingeboren werden C(2), bilden, konstruieren und konstituieren wir eine in der Person, im Subjekt, in uns bestehende (subjektimmanente) Er­kenntnis der "Außenwelt". Für jeden Ungewohnten erscheint es ein wenig kühn, wenn er hört: "Ich weiß gar nicht, wie die 'Außenwelt' aussieht, denn was ich von ihr weiß, ist nichts als ein Bild, ein Konstrukt, das ich mir davon mache. Ich sehe nur, was in meinen Augennerven ist, aber nicht die Abend­sonne, die ein Blatt durchleuchtet."

Nur das Angewirktsein der Sinne durch die "Außenwelt" kommt von außen, alle übrigen Tätigkeiten sind aktive, erzeugende Handlungen im Bewusstsein des Men­schen. Die ge­naue Unterscheidung von D(1) und D(2) ist dabei ebenso wichtig wie die Unterschei­dung der Begriffe, die schon bei Geburt ge­geben sind, von jenen, die über die Gesellschaft und deren Sprache im Rahmen der Sozialisation erworben werden. Da je­der in einer sozialen Umwelt geboren wird, die durch die Faktoren der Gesell­schaft (wie z. B. Sprache, Kultur, Wirtschaft, Politik, Schichtung) bestimmt ist, tritt eine Einwir­kung aller dieser Faktoren auf E, D und C ein, die zu einer Kanalisierung und Regulierung, entsprechend den Färbungen der Gesell­schaft, führt.

Die Probleme der Erkenntnis der Außenwelt über die Sinne wollen wir jetzt ausführ­licher behandeln.

1.2.1 Erkenntnis von Außenwelt

1.2.1.1 Äußerlich sinnliche Erkenntnis mittels E, D(1), D(2), C, B, A

Für die Kenntnis der Welt um uns brauchen wir einen Leib. Der Zustand der Sinnes­organe, also der "Stempel", den das Außen auf ihnen erzeugt, ist alles, was von außen ist. Ein Blinder er­hält auf der Netzhaut keine "Spuren". Er lebt daher in einer "anderen" Welt.Wir zitieren im folgenden, oft leicht verändert, aus den er­kenntnistheoretischen Schriften KRAUSEs.Von diesen Zuständen in den Sinnen behaupten wir, sie seien Wirkungen äuße­rer, "wirklicher" Gegenstände, die in Raum und Zeit sind, die mit unserem Leib, also mit Augen, Nase, Oh­ren, Haut usw., in einer Wechselwirkung stehen, wobei aber diese Sinnesorgane bei der Erzeugung dieser Empfindungen selbst auch aktiv mitwirken. Wir behaupten dann auch gleich – eigentlich sehr kühn –, dass einerseits diese Gegen­stände auch unabhängig davon, dass sie in unseren Sinnen Wirkungen er­zeugen, exi­stieren und dass sie andererseits unabhängig von unserer Sinnlichkeit und unserer Fähigkeit und Möglichkeit, sie wahrzunehmen, gegeben sind.Allgemeine Bedingungen für die Sinneswahrnehmung sind:1.     Ein organischer Leib, seine Sinnesorgane, das Nervensy­stem, durch welches alle Sinnesorgane unter sich mit dem gesamten Nervensystem und mit dem ganzen Leib in Verbindung stehen (Koordinierungs– und Integrierfunktion des Nervensystems und des Hirns). Einzelne Sinne können manchen Menschen fehlen, kein einziger aber allen. Die "Welt" würde sich schlagartig ändern, wenn alle Men­schen plötzlich taub wären.2.     Dasein und Wirksamkeit der unseren Leib umgebenden Sinnenwelt, wobei wir auch noch annehmen können, dass die "Naturprozesse", die in unserem Körper ablaufen, wenn wir die Natur erkennen, zu den "Naturprozessen außerhalb unser" in einem bestimmten Verhältnis stehen.3.     Schließlich müssen wir uns den Sinneseindrücken hinge­ben, hinmerken, darauf acht geben.Jeder Sinn stellt ihm Eigentümliches dar. Die Bestimmung der Größe und des Grades der Anwirkung ist für die Wahrnehmung wichtig.

1.2.1.1.1 Der Tastsinn

Hauptsitz im Organ der Haut, besonders Zunge und Fingerspit­zen. Jeder Nerv aber ist Teil des Tastsinns. Der Tastsinn ist der allgemeinste Sinn, der sich auf die allge­meinsten Eigenschaften der Körper, auf den Zusammenhalt in festem und flüssigem Zustand nach Wärme und Kälte bezieht. Die Anwirkungen halten in ihm am relativ längsten an, er ist aber der beschränkteste Sinn, denn man muss ja "den Gegenstand" selbst berühren. Man nimmt auch im Verhältnis zu anderen Sinnen mit dem Tastsinn die kleinste Mannigfaltigkeit wahr. Wir nehmen im Tastsinn nur Zusammenhaltbestimmtheiten des Tastnervs selbst wahr, mögen sie nun mechanisch oder durch Erwärmung und Erkältung erfolgen, wobei sich eine große Mannigfaltigkeit einzelner besonderer Empfindungen ergibt. Fast jede dieser weiteren Bestimmtheiten des Tastgefühls zeigt durch das Gefühl von Lust und Unlust eine wesentliche Bezie­hung zum Leib. In diesem Sinne gibt es einen weiten Bereich von Gradverschiedenheiten, wodurch dieser Sinn zur Orientie­rung in der äußeren Sinnenwelt und zur Untersuchung der Or­gane des eigenen Körpers hinsichtlich der Kohäsion besonders geeignet ist. Mittelbar aber schließen wir von den unmittelbar wahrgenommenen Kohäsionsbestimmtheiten unserer Nerven auch auf Ge­stalt, Ort, Stelle und Bewegung desjenigen Stoffes, welcher die wahrgenommenen Kohäsionsbestimmtheiten unseres Nervs innerhalb der Wechselwirkung dieses Gegenstandes mit allem ihn um­gebenden Leiblichen verursacht. Dies erreichen wir aber nur durch Schlüsse. Bei dieser Aus­legung des Tastgefühls dienen uns als Grundlage bestimmte, nichtsinnliche Begriffe, Urteile und Schlüsse (C in FIGUR 1), die wegen der Allgemeinheit und Allgemeingültigkeit, die wir ihnen beimessen, nicht aus der Sinneswahrnehmung entsprungen sein können.

Solche Begriffe sind etwa: Das Gefühl im Tastsinn ist weder lang, noch breit, noch tief, ist gar kein Stoff. Daher müssen wir diesen Gedanken schon unabhängig von dieser Empfindung des Tastgefühles haben, wenn wir behaupten, einen Stoff wahrzunehmen. Fer­ner bringen wir den Gedanken der Bewegung hinzu, denn auch dieser liegt nicht in dem einfachen Gefühl. Bewegung können wir nicht an­schauen ohne Zeit, weil Bewegung Änderung ist. Folglich bringen wir auch den Gedanken der Zeit hinzu. Nun beobachten wir aber, dass wir uns mittels dieser Gedanken des Räumlichen und Zeitlichen in unserer Phantasie dasjenige vorstellen, woran wir diese Empfindung als seiend denken und wodurch wir sie uns als verursacht vorstellen. Dies wird recht offenbar, wenn man sich einen Blinden denkt oder wenn man sich selbst denkt, wie man sich an finsteren Orten durch das Gefühl weiterhilft. Da kann man weder seinen Leib noch das Äußere sehen. Trotzdem wird das be­stimmte einfache Tastgefühl Anlass dazu, dass sich der Blinde, der geblendet Sehende oder der Mensch im Finsteren innerlich in Phantasie (D in FIGUR 1) ein Bild vom Äußeren entwirft, das ihn umgibt. Nun beinhaltet aber das, was der Blinde, der Geblendete oder der Mensch in Dunkelheit mit tastenden Händen erspüren, we­der Raum noch Stoff, auch erkennen diese gar nicht durch das Gesicht, und dennoch bilden sie diese innere Welt der Phantasie. Sie behaupten, dies geschehe der äußeren Welt entsprechend. Daraus sehen wir, dass das Vorhandensein der Welt der Phantasie (D) und unser freies Schaffen darin auch eine Grundbedingung dafür ist, dass wir die einzelnen Tastge­fühle auf Raum und Materie beziehen können.

Aber bei dieser Auslegung des "dumpfen" Tastgefühles sind noch viel höhere Voraussetzungen erforderlich, und es sind dabei viel höhere geistige, kognitive Verrichtungen wirksam als nur die Welt der Phantasie, die wir weiter unten noch ausführlich analysieren werden. Denn wir müssen ganz allgemeine Begriffe, Urteile und Schlüsse (C in FIGUR 1) – z. B. "etwas", "etwas Bestimmtes" – hinzubringen, von wel­chen die einfache Empfindung des Tastgefühls gar nichts enthält. Hätten wir einen solchen Begriff nicht, so könnten wir gar nicht den­ken, dass wir etwas fühlen oder etwas durch Gefühl wahrnehmen. Weiterhin benützen wir den Gedanken "Eigenschaft", indem wir die Tastempfindung als Eigenschaft dessen, was wir im Ge­fühle wahrnehmen, betrachten. Überdies verwenden wir die Begriffe: Ganzes, Teil , Verhältnis, Beziehung, Grund und Ur­sache. Denn wir denken ja, dass das äußere Objekt und unsere Sinne Grund und Ursache dieser Empfindung sind. Wir benüt­zen aber auch Urteile und Schlüsse. Zum Beispiel: "Hier ist etwas, ein Objekt; hier ist eine Wirkung; hier ist eine Empfindung." Demnach muss die Empfindung, wie alles Bestimmte, eine Ursache haben. Da ich selbst nicht die Ursache bin, folglich muss etwas anderes da sein, was Ursache der Empfindung ist. Hier ist eine Eigenschaft, also muss etwas sein, woran die Eigenschaft gebunden ist, etwas im Raum Selbstän­diges, das auch in der Ausdehnung über längere Zeit anhält.

Diese Begriffe, Urteile und Schlüsse sind uns bei der Auslegung des Sinnes in unserem gewöhnlichen Bewusstsein so geläufig, wir wenden sie mit so großer Kunstfertigkeit an, dass wir uns derselben nur selten bewusst werden. Durch diesen Umstand des Nichtbewusstwerdens dieser Voraussetzungen lassen sich viele verleiten zu behaupten, die Aner­kenntnis der äußeren Gegen­stände mittels der Sinne sei unmittelbar, und zwar geschehe sie auf eine uns unbegreifliche Weise. Aber wer auf sich selbst hinmerkt, der findet, dass es so geschieht, wie wir hier feststellten. Und wir dürfen unser gebildetes Bewusstsein, das sich bereits eine kunstfertige Beherrschung unseres Leibes erworben hat, nicht mit dem Zustande des Kindes verwechseln, welches sich erst jene Fä­higkeit nach und nach erwerben muss. Bei dieser geistigen Arbeit können wir auch die Kinder be­obachten. Es geht uns in unserem reifen Bewusstsein mit der Auslegung der Sinne so wie einem Weber oder Orgelspieler. Wir bringen die kognitive Tätigkeit und die Tä­tigkeit unserer Phantasie, während wir sie durchführen, nicht ins Bewusstsein, weil wir sie schon beherrschen. Wie sich auch der Orgelspieler dessen nicht bewusst wird, wie er die Noten sehen, verstehen und durch ganz bestimmte geistige Tätigkeit seine Finger und Füße bewegen muss. Wenn aber der Orgelspieler oder der Weber sich an die Zeit erinnert, wo er die Kunst erst erlernte, so wird er sich auch erin­nern, wie er sich anfänglich je­der dieser Tätigkeiten bewusst werden musste, wie er alles einzelne einzeln einüben musste, um endlich zur Kunstfertigkeit zu gelangen. Ein sol­ches aber noch viel höherartiges Instrument als die Or­gel dem Orgelspieler ist jedem Bewusst­sein (jeder "kognitiven Instanz") der Leib. Erst nach und nach werden wir des Leibes mächtig, erst nach und nach lernt der Mensch die Sinne ver­stehen und seinen Leib zu gebrauchen.

Wir können uns z. B. in einem finsteren Keller beim Tasten im Dunkeln täu­schen. Was täuscht sich da? Die Wirkung auf den Tastsinn ist wie immer. Aber wir legen diese Eindrücke falsch aus, wir machen uns "falsche Bilder" von dem, was wir da ta­sten, und wir schließen falsch auf das, was da "draußen" ist. Wir können uns auch z. B. bei Helligkeit täuschen, wenn wir sitzen und plötzlich einen Druck am Fuß ver­spüren. Wir wissen dann nicht, ob wir angestoßen wer­den oder ob es ein Gegen­stand ist, den jemand an den Fuß gebracht hat. Hier sei auch erwähnt, dass man natürlich einwenden könnte, die Gedanken, Begriffe usw., die hier zur Auslegung der Sinne benützt werden, hätten wir nicht ursprüng­lich, sondern Be­griffe, Urteile und Schlüsse (also C in FIGUR 1) lernten wir erst durch eine Sprache in einem Gesellschaftssystem. Zum einen legt aber das Kind, wie wir sehen, die Sinne schon aus, bevor es sprechen lernt. Ja das Erlernen einer Spra­che ist selbst ein Vorgang der Auslegung der Sinne mittels Begriffen, Urtei­len usw. – also mittels "kognitiver Strukturen". Das Kind legt hierbei Sinneseindrücke (Laute und Zeichen) so aus, dass es darin Elemente und Zeichen erkennt, die über die sinnli­che Dimension hinaus

etwas anderes bedeuten (Erkennung der Be­deutungsdimension von Zeichen). Ein Kind hat also schon C-Begriffe bevor es C(s) -Begriffe, C(s) -Urteile einer Sprache lernt. Eben weil das Perlhuhn das nicht kann, obwohl es auch Sinne hat, kann es unsere Sprachen nicht erlernen. (Vgl. Pflegerl: Voll­endete Kunst S. 4 f. und S. 109.)

Wir müssen weiterhin unseren aktiven Einsatz des Tastsinnes be­achten. Wir lie­gen nicht irgendwo und lassen die "Dinge auf uns einwirken", sondern wir be­wegen ja unseren Körper, um seine Tastempfindungen gezielt, intentional auf etwas Hartes, auf eine Gegenwirkung hin, eben auf einen "Gegenstand" zu rich­ten, etwas abzuta­sten. Wir veranlassen unseren Körper zu Bewegungen. Auch hier spüren wir in den Tastnerven das He­ben des Armes, die Bewegung des Fußes, und wir spüren das An­stoßen, die "Eigenschaften" des Körpers. Wir steuern auch Richtung und Stärke der Bewegung, z. B. des Tastens. Wir kön­nen durch diesen aktiven Einsatz des Tastsin­nes unseren eige­nen Körper mit Zunge, Händen und Füßen in absichtlicher Be­obachtung kennen lernen. Wir werden uns damit der Teile un­seres Körpers und sei­ner Gestalt in gleicher Weise wie der "Gegenstände" außerhalb des Leibes bewusst.

1.2.1.1.2 Geschmackssinn

Der Geschmacks- wie auch der Geruchssinn kommen dem Tastsinn insofern nahe, als auch bei ihnen stoffliche Berührung nötig ist. Die Angewirktheit, der "Stempel", der hier in den beiden Sinnen wahrgenommen wird, ist die Be­stimmtheit des che­misch-organischen Stoffes im Sinnesorgan selbst. Die Emp­findung des Schmeckens enthält eine große Mannigfaltigkeit, mit starken Ten­denzen einer begleitenden Lust- oder Unlust­empfindung (Ekel beim Essen be­stimmter Stoffe; Verfeinerung und Dif­ferenzierung der Geschmacks"kultur"). Wir nehmen schmeckend nur die chemische Tätigkeitsstimmung unseres Or­gans, der Zunge, wahr, keineswegs aber einen äuße­ren Ge­genstand selbst noch dessen chemische Beschaffenheit. Aber wir übertra­gen das Wahrgenommene nach den gleichen Vor­aussetzungen wie unter 1.2.1.1.1 auf die Au­ßenwelt. Auch hier benützen wir zur Erzeugung der sinnlichen Erkenntnis Phanta­sie D und be­griffliche Operationen C und C(s).

Gedankenmodell: Jemand muss etwas mit verbundenen Augen essen und fest­stellen, was es ist; oder wir stellen uns vor, wie ein Rindsbraten mit Kartoffel­salat schmeckt. Ein Österreicher kann sich aber in der Regel nicht vorstellen, wie Imam Bayildi schmeckt.

1.2.1.1.3 Geruchssinn

Der Geruchssinn ist bereits freier als der Geschmacks– und Tastsinn. Man kann auch von fern Gerüche wahrnehmen. Auch der Tastsinn ist fein und mannigfal­tig, womit neue Schlüsse auf die Beschaffenheit von Körpern oder Erscheinun­gen in der Natur möglich sind (z. B. bei einem Rasenbrand oder Ölteppich auf dem Meer). Erinnert sei hier an den Versuch, in Filmen eine Geruchsdimension zu integrieren.

1.2.1.1.4 Gesichtssinn

Er ist unter allen Sinnen der freieste, von Lust und Unlust des Körpers unab­hängigste, das Organ des Auges selbst ist rasch und vielseitiger orientierbar. Unmit­telbar sehen wir keine Welt außerhalb unser, sondern nur auf der Fläche des Auges Be­stimmtheiten des Lichts an Helle und Farbe. (Auch dies sind schon sehr abstrakte Konstruktionen mit Begriffen und durch Phantasie.) Aber durch die sprunghaften, ganz oder teilweise scharf begrenzten Umrisse mehr oder we­niger durchsichtiger Körper sowie durch die mittels der Schatten und des abge­strahlten Lichtes bestimm­ten, allmählichen Übergänge der Helligkeit und der Farben begründet das Bild im Auge die weiteren Schlüsse auf die Lichtbe­stimmtheiten und Beschaf­fenheiten der Gegenstände und auf deren Gestalt, Ort, Stelle und Bewegung. Bei der Auslegung des Bildes im Auge kommt der be­reits ausgelegte und richtig verstandene Tastsinn dem Bewusstsein erheblich zu Hilfe (integrative Koordinierung der Auslegungsergeb­nisse aller Sinne in den kognitiven Leistungen des Bewusstseins). Dass es aber nur unser erleuchtetes, farbig bestimmtes Auge, eigentlich eine "physio-chemische Reak­tion", ist, was wir äußerlich sinnlich sehen, wahrnehmen und unter Anwendung nichtsinnli­cher Voraussetzungen C und mit Hilfe von Phantasie D auslegen, zeigt uns fol­gende Tatsache: Vernichtung und Krankheit des Organs vernichtet oder verän­dert das Sehen; sind die Augen verbunden, sehen wir nichts. Folgende Erscheinungen können als weitere Denkanstöße für diese komplizier­ten Zusammenhänge dienen: Jedes Auge gibt ein besonderes Bild; solange wir nicht ein Auge schließen, ko­ordinieren wir die beiden Bilder zu einem Doppel­bild; Schwin­del bei Aufsetzen einer schlechten Brille; Farbenblindheit; bei Sto­ßen oder Drücken des Auges auftretende Lichterscheinun­gen; optische Täu­schungen; Zusammensehen schnell bewegter Bilder im Film; perspektivische Verzerrung in die Ferne hin; Benützung dieser Eigenschaften in der Zentralper­spektive der Malerei; Verzerrung durch Gläser; Benützung von Brillen bei Seh­fehlern oder Sehschwäche; Teleskope; Mikroskope; Repro­duzierung des Sehvor­ganges in Fotografie, Film, Video, wo wie­derum nur Sinnesdaten des Auges ausgelegt werden. Hier ein wichtiger Einschub über die Grenzen der Beobacht­barkeit der Natur in der Naturwissenschaft: Werden Mikroer­scheinungen in der Natur mit Licht be­obachtet, wird durch die Wirkung des Lichtes des Beobachtungsvorganges der beob­achtete Be­reich verändert: Der Vorgang der Beobachtung selbst verändert das zu Beob­achtende, das Beobachtete "verschwindet" in eine neue Konstella­tion. Beachten wir aber weiter. Wir sehen ja nicht diesen Mikrobereich, wie er wirklich ist, wir ma­chen uns ja nur aus Zuständen in den Augen E mit Phantasiebildern D und Begriffen, z. B. der wissenschaftli­chen Theorie C(T), ein inneres Bild von der Sache. Nun die entscheidende Überle­gung: Nicht nur durch die Lichtstrah­len, die wir auf das Beobachtungsobjekt lenken, wird verän­dert, was wir be­obachten, sondern auch durch eine Verände­rung in den Begriffen C(T) und in den Phantasiebildern D wird unsere Beobachtung, das Beobachtungser­gebnis verän­dert. Es "verschwindet" das eine Bildergeb­nis, und es ergibt sich ein anderes. Hinzu kommt: Wir können das Bild, das wir uns in der Beobach­tung gemacht haben, niemals mit der Wirklichkeit außerhalb unser verglei­chen, wir können nicht feststellen, ob unser Bild dem entspricht, was außer­halb unser ist, denn wir kommen niemals hinaus zu den Dingen, wir können nur verschiedene Bilder in uns miteinander verglei­chen.

In den letzten Zeilen haben wir zwei wichtige Grundsätze er­wähnt:

·       Das Problem der Relativität jeglicher naturwissenschaftli­cher Erkenntnis, weil sie von den eingesetzten Begriffen C und den Phantasiebildern D ab­hängig ist, und

·       das Problem, dass wir die Wahrheit naturwissenschaftli­cher Erkenntnis über­haupt nicht durch einen Vergleich zwischen unserer Erkenntnis und einer "objektiven" Au­ßenwelt überprüfen können. Beides wird uns weiter unten noch beschäftigen.

1.2.1.1.4.1 Vergleich Retina – Computer

"Um nur 100 Millisekunden der Arbeit einer einzigen Nerven­zelle der Retina in ei­nem Rechner zu simulieren, müssten gleichzeitig 500 nichtlineare Differential­gleichungen hundert­mal gelöst werden. Auf einem der schnellsten Computer, dem Superrechner CRAY, würde dies mehrere Minuten Rechenar­beit beanspru­chen. Um­gerechnet auf die normale Funktion der Retina pro Sekunde, benötigte der Super­rechner mindestens 100 Jahre (EBELING)."

1.2.1.1.4.2 "Ich sehe eine Rose"

Für das Verständnis der Beziehung zwischen DI und MI ist be­reits die sorgfäl­tige Analyse dieser hochkomplexen Vorgänge bei der Erkenntnis der Außenwelt bedeu­tungsvoll. Darum noch ein Hinweis: "Ich sehe eine Rose", sagt man. Das unmittelbar Wahrge­nommene der sinnlichen Erkenntnis ist hierbei lediglich dieses be­stimmte flächige Bild im Auge E. Aber sogleich bearbeite ich das Bild weiter, indem ich dasselbe durch Phantasietätigkeit gleichsam plastisch vollende, wobei ich dann auch früher durchge­führte Anschauungen davon er­neuere und aktiv mit Phantasie hinzufüge, was ich sonst schon einzeln sinnlich in Erfassung der Rose erkannt habe. Ich besitze sodann eigentlich ein vereintes Bild aus dem reinen Augenbilde und dem Phantasiebilde, wobei ich aber dieses vereinte Bild für das Bild der Rose selbst halte. Ich glaube also, dies alles soeben an der Rose selbst zu erblicken. Ich vermeine, die Far­ben, die in meinen Au­gennerven wahrgenom­men werden, als an der Rose selbst haftende und als außer­halb meines Leibes an dem Ort, wo die Rose selbst ist, vorhandene wahrzu­nehmen. Aber auch dabei lässt es das denkende und schauende Bewusst­sein nicht be­wenden, sondern es trägt dieses Vereinbild, ein plastisch raumzeitliches Phan­tasiebild im Bereiche D(1), in welches es seine reinsinn­liche Anschauung aufgenommen hat, dann wieder hinaus in die angeblich äußere Natur.

Indem ich die Rose an einem Rosenstock erblicke, der vor mir in einem Garten steht, trage ich das innerlich vollendete Ver­einbild davon auch im Bewusstsein hinaus. Ich proji­ziere das Bild hinaus, ich sage mir: "Das Bild ist nicht in dir, es ist au­ßer dir 'im Gar­ten.'" Ich trage es hinüber an diese bestimmte Stelle im Raum und eben dann, wenn der Mensch dies in seinem "vorwissenschaftlichen Be­wusstsein" voll­bracht hat, meint er, er habe den Gegenstand selbst gesehen und wahrgenommen.

1.2.1.1.5 Gehörsinn

Der Gehörsinn nimmt im Inneren des Ohres die Bestimmtheit der inneren, stoffli­chen Selbstbewegung (Vibration) des Hör­nervs wahr. Auch hier legen wir diese sinn­liche Bestimmtheit E mit Phantasie D und Begriffen C aus und ma­chen uns ein Bild von dem, was klingt, lärmt, quietscht usw. Die Schallbewegung enthält in sich mannigfaltige Bestimmt­heiten, z. B. Artver­schiedenheit der Stimmen, Laute, Höhen und Tiefen, Stärke oder Schwäche; men­schliche Musik ist eine ak­tive Erzeugung sinnlicher Schallqualitäten; beim Bau von Mu­sikinstrumenten benützt man bestimmte Tonsysteme, wo ma­thematische Rela­tionen maßgeblich sind. Erwähnt seien be­stimmte Gesellschaf­ten, in denen Sprache nur als gesprochene, nicht als geschriebene Sprache vor­kommt (orale Kultur), also Gesellschaftssysteme, in denen der Gehörsinn stär­ker aktiviert wird als in Systemen mit Benutzung der Schriftsprache.

1.2.1.2 Integrative Koordinierung der Zustände, "Daten" aller Sinne

Jeder einzelne Sinn ist selbständig und eigentümlich. Aber das wahrnehmende Be­wusstsein verbindet in Phantasie D die Wahrnehmungen jedes einzelnen Sin­nes mit Hilfe der erwähn­ten begrifflichen Operationen C in ein Ganzes der Wahrneh­mung und bezieht sie alle auf die gleichen einzelnen Gegen­stände in der äußeren Natur. Diese integrierende, synthetisie­rende Koordinierung und Verbindung des Einzelnen zu einem Gesamten ist ein wichtiger kognitiver Akt. Hinsichtlich dieser Koordinierungsfunktion ein interessantes Beispiel: In dem Kurz­film "Die Täuschung des Auges durch das Ohr" von Andreas KOPRIVA wird eine Szene einmal ge­dreht, dreimal kopiert und jeweils mit anderen Ge­räuschen und Dialogen synchronisiert, wodurch sich bei gleichen optischen Sin­neseindrücken durch die Variation der auditiven "Eindrücke" drei unterschied­liche Wirklichkeiten ergeben. Wir sehen hier, dass uns die Außenwelt nicht direkt zugänglich ist. Die Sinne unseres Körpers sind gleichsam der Filter und das Stempelkissen, auf welche sie wirkt. Wir sehen die erhebli­chen konstruktiven und koordinierenden Lei­stungen der Phan­tasie D und der kognitiven begrifflichen Operationen, mit denen wir uns in uns ein Bild von außen machen, dabei aber auch noch glauben, wir erlebten die Welt außerhalb unser, wie sie ist. Bereits an diesem Punkt un­terscheiden sich die ver­schiedenen philosophischen Systeme bei der Beantwor­tung der Frage, wie diese Tatsache ei­gentlich zu verarbeiten sei. Wir le­ben ja in einer konstruierten inneren Bildwelt. Vor allem erhebt sich die Frage: Wie kön­nen wir wissen, ob das, was wir derart von der Welt erkennen, auch wahr ist (Wahrheitsproblematik)?

1.2.2. Phantasiewelten D

1.2.2.1 Äußere Phantasie D(1)

Wir haben im Vorigen gesehen, dass Sinnes"stempel" der Sin­nesorgane mit der Phan­tasie verbunden werden und die Phanta­sie – natürlich unter Benützung von Begrif­fen, Schlüssen usw. – Bilder der äußeren Welt erzeugt. Wir wollen diese Phantasietä­tigkeit etwas schlampig als äußere Phantasie D(1) bezeichnen. D(1) erzeugt eine mit der äußeren Sinnenwelt E integrativ ge­bildete Phantasiewelt. Damit ist aber im Bewusst­sein der Be­reich der Phantasietätigkeit bei weitem nicht erschöpft.

1.2.2.2 Innere Phantasie D(2)

Wir stellen fest, dass es ohne weiteres möglich ist, Bilder in D(1) in der Phanta­sie weiterzubilden. Wir können in der Phan­tasie Bäume bilden, auf denen Sil­berpferde hängen, Menschen mit Vogelköpfen, Phantasiewesen, wie die Turtles, Donald Duck, Asterix, Pokemon, die Bilderwelt eines Malers wie DALI oder MAX ERNST. Wir können uns in der Phantasie das Haas-Haus auf dem Mund einer Frau, kombiniert mit dem Geruch von Schokoladekeksen und den Klängen einer Arie der Oper "Tosca" vorstellen. Phantasiebilder sind natürlich nicht auf den Ge­sichtssinn beschränkt. Die Traumfa­brik Hollywood erzeugt unentwegt Bild­welten, die mittels Phantasie aus der Natur und den Gesellschaften nachgebil­det und weitergebildet sind und die in zunehmen­dem Maße über die Kinos der ganzen Welt in die Phantasiewelten der Konsumenten übergehen. In unserer Phantasie kann es aber auch Formen geben, die in keiner Weise aus der Natur weitergebildet sind. In dem Buch "Die Vollendete Kunst" habe ich gründlich aufgezeigt, dass in der modernen Malerei der entscheidende Schritt vollzogen wurde, Formen unabhängig von der Natur zu finden und darzu­stellen. MAX BILL sagt:" Konkrete Kunst nennen wir jene Kunstwerke, die aufgrund ihrer ureigenen Mittel und Gesetz­mäßigkeiten – ohne äußerliche Anlehnung an Naturerscheinun­gen oder deren Transformierung, also nicht durch Abstraktion, – entstanden sind. "Es gibt also unendlich viele Möglichkeiten der Erzeugung von Formen in der men­schlichen Phantasie, die nicht aus den Phantasiegebilden D(1) abgeleitet sind, die wir aus der sinnli­chen Erkenntnis gewinnen. Die Entwicklung der Kunst seit 1910 bietet reiche Beispiele. Es ist auch zu beachten, dass wir zur Erstellung bestimmter Phantasiegebilde über­haupt keiner sinnlichen Eindrücke E be­dürfen; die Sinnlichkeit ist also nicht Vor­aussetzung unserer Phantasiefähigkeit.Ist die Phantasie in D(1) schon bei der Erzeugung sinnlicher Erkenntnis aktiv und innovativ, so ist sie in der Erzeugung von Phantasiegebilden in D(2) noch wesentlich freier. Selbstver­ständlich werden auch bei der Erzeugung von Phantasiegebil­den in D(2) Begriffe usw. eingesetzt, wenn etwa der Maler, der Architekt oder Erfinder neue Formen sucht. Wir beobachten aber auch, dass wir ständig die beiden Bildwelten D(1) und D(2) miteinander verbinden und dass vor allem in allen gesellschaft­lichen Berei­chen, von der Finanzverwaltung bis zum elektroni­schen Spielautomaten, ständig durch Neubildungen in D(1) und D(2) und deren Verbindungen Veränderungen in die "Außenwelt" gebracht werden.Den Aufsatz über die Grundlagen digitaler Kunsttheorie von Ernst Riemschneider:  "Deduktive Kunst – Digitalisierung" möchte ich hier zur Verdeutlichung benützen. Es wird näm­lich bei der Frage der DI sehr darauf ankommen, festzustellen, ob diese mit hohen Frei­heitsgraden, in Verbindung mit dem Einsatz von Begriffen C in unserem Be­wusstsein erzeugten Phantasiewelten D(1) und D(2) in gleicher Weise von Compu­tern er­zeugt werden können. Es würde nämlich nicht genügen, dass der Rechner von irgendwel­chen Menschen bereits dargestellte Bilder nach­machen kann, sondern es ist zu fragen, ob er mit der gleichen Spontaneität, in der gleichen Form und Vielfalt neue Phantasiewelten er­zeugen kann. Diese Phantasiegebilde müssten aber in der glei­chen Weise neu sein, wie etwa die Bilder von MAX ERNST oder GOYA in der Malgeschichte neu waren. Es geht also um einen Grad von Neuartigkeit, der genau bestimmt sein muss. Denn es ist klar, dass z. B. manche Maler neue Bilder ma­chen, die in auffälligem Maße jenen von MAX ERNST glei­chen. Sie ahmen nur eine Er­findung nach, die dieser Maler erstmals vollzogen hat. Wir meinen hier also nicht die nachahmende Neuschöpfung in der Phantasie, sondern eine bestimmte, dar­über hinausgehende Art der Neuheit (Innovationsdimension) Vgl. den Be­griff der "Originalität" bei PENROSE, S. 414.

Nun zum Aufsatz Ernst Riemschneider:  "Deduktive Kunst – Digitalisierung". Text und Bilder sind bereits mittels digitaler Soft­ware erstellt (PAINTBRUSH-Programm). Die dargestellten Bilder hatte der Au­tor vorher in seiner Phantasie D(2). Wir wollen einige analysieren: Die Bilder von Flächen unter 2.2 und von Linien unter 2.3 sind, wie der Text zeigt, mit Begriffen mathematischer und logischer Art verbunden, die mit unse­ren bisher behandelten Erkenntnis­operationen nicht zusammenhängen. Es liegt also eine hoch­gradige Verknüpfung der Bilder mit Begriffen vor, die mit sinnli­cher Erfahrung nichts zu tun haben. Eigentlich setzen die­selben eine mathema­tische Axiomatik vor­aus, von der dann eben Skizzen in der Phantasie abgebildet werden. Man kann diese Bilder unter 2.2 und 2.3 erst " verstehen", wenn man diese mathematischen Axiome ver­standen hat, was aber allein durch Phantasie D gar nicht möglich ist. Wir können nämlich z. B. nicht den "ganzen Gedanken" der unendlichen Linie in der Phantasie nachbilden, weil die Phantasie nur Endli­ches nach­bilden kann. Ob und wie wir Un­endliches denken können und dürfen, müssen wir erst später überprüfen. Das gleiche gilt von der Kochschen Kurve. Eine fraktale Ähnlichkeitsfunktion ist eine mathema­tische Relation, die wie­derum durch digitalisier­bare Programme grafisch darstellbar ist. Wir können bis zu ei­nem gewissen Grad in Phantasie D(2) die Entwicklung der Kurve nach­bilden; niemals aber vollständig, da die Teilung ja unendlich fortsetzbar ist.

Wir können uns in der Phantasie D(2) eine Vielzahl der Orna­mente unter 4.1.2 nachbilden. Auch diese Ornamente sind nicht aus der Außenwelt mit Sinnes­eindrücken gewonnen, sie kön­nen, wie wir zeigen, mit einem BASIC-Programm er­zeugt wer­den. Auch hier sind die Grundlagen der Phantasiebilder in D(2) ver­bunden mit "allgemeinen" Begriffen, wie "Allheit", "Stufung", "Inversion", "Spiegelung", "Regelmäßigkeit", "Selbheitlichkeit", "Ganzheitlichkeit" und "Harmonie". Beach­ten wir auch, dass wir normalerweise Schwierigkeiten haben, uns solche 8X8-Ornamente in größerer Zahl zu merken. Ein Schachmeister ist jedoch in der Lage, eine Vielzahl von 8X8-Konstellationen lange in Erinnerung zu behalten.Die Bilder ab OR-OM0.PCX sind deshalb um eine Stufe kom­plexer, weil alle Striche, Füllungen von Flächen usw. mit Mu­stern (pattern) gezeichnet sind, die unter 4.1 er­zeugt wurden. Für die Erzeugung dieser Bilder in D(2) wurde eine Vielzahl von be­grifflichen und theoretischen Grundlagen herangezogen, die alle als Sinnebenen, als Sinn­gehalte, als inhaltliche Im­plikationen in den Bildern enthalten sind. Man "versteht" die Bilder also erst dann richtig, wenn man diese theoretischen Grundlagen, die nicht in der Phanta­sie gelegen sind, mitbe­rücksichtigt. Es sind dies u.a.:

·       die im Buch "Vollendete Kunst" dargelegte Grundwis­senschaft,

·       die in OR-OM1.PCX angedeutete und hier unter 1.2.3.1.1 entwickelte Philo­sophie der geraden Linie, inklusive der logischen und mathematischen Axiomatik derselben.

·       Die Einhaltung einer Gliederung der Bilder, die dem "Gliedbau des Welt­alls" ähnlich ist.

·       Die potentielle und virtuelle Benützung aller bisherigen Bilder der Kunst­geschichte, die nach den Prinzipien der "Vollendeten Kunst" als Material zur Er­zeugung neuer, komplexer, den neuen Baugesetzen entsprechender Bilder im Ge­samtbau der Malerei einen bestimmten "logischen" Platz ein­nehmen (integrative Synthesen mit neuen Prinzi­pien).

·       Die Aufnahme aller bisherigen theoretischen Ansätze der Kunstentwicklung in den Allzusammenhang der neuen Axiomatik.Was stammt bei diesen Bildern der Phantasie D(2) aus der Sinnlichkeit E, was aus der äußeren Phantasie D(1)? Der Autor hat Bilder aus der Kunstgeschichte, die Phi­losophie der Grundwissenschaft, die bisherigen Theorien der Logik, Ma­thematik und Malerei als Sinneseindrücke – "Bilder" oder "Zeichen mit Bedeu­tung" – aus Büchern durch Einsatz von Be­griffen C und Phantasie D aufge­nommen. Hieraus wurden als eine komplexe Synthese durch eine Vielzahl von Begriffsope­rationen mit C, in Ver­bindung mit D und E und dem Einsatz von "äußeren" Werkzeugen wie einem PC und seiner Soft­ware diese Bilder herge­stellt, die der Leser wiederum nur als Sinnes­qualitäten auf seiner Netzhaut vor­findet. Der Zeichner der Bilder kann sich etwa "alle Einzelheiten" des BildesOR-OM27.PCX, also die Stellung eines jeden Pixel im Raster, nicht merken. Auf der Festplatte seines PC wie auch auf Dis­ketten im Club sind jedoch alle De­tails digital aufgezeichnet, genauso wie man früher in Schriftstücken Informa­tionen speicherte.Wir können in Phantasie D(2) Einzelbilder aus einem Zusam­menhang nehmen und in andere setzen. Die Montagetechnik in der Malerei hat dies auch in "äußeren Bil­dern" angewandt. Im PAINTBRUSH-Programm ist eine Funktion vorgesehen, "einfache Bilder" wie OR-OM2.PCX in andere, komplexere Bilder einzubauen ( paste-Funktion). Weiterhin können Bilder der "Außenwelt" in Büchern durch einen Scanner eingelesen und in andere Bilder eingebaut werden (z. B. in OR-OM65.PCX). Der kom­plizierte Vorgang, dass man beim Erzeugen "äußerer" Bil­der auf dem Monitor nicht immer nur Bilder der inneren Phan­tasie – in Ver­bindung mit jenen der äußeren – in das neue Me­dium "umsetzt" oder "herauskopiert", sondern dass man durch Pro­bieren mit Elementen und CUT-fi­les im Zeichenprogramm selbst plötzlich einem bis­her nicht bekannte, in der Phantasie D(2) noch nicht gegebene oder konstruierte Bil­der erzeugt, die man sich dann wieder merkt, also in D(1) und D(2) aufnimmt, kann hier nicht im De­tail untersucht werden.

1.2.3 Begriffswelten (Logik, Mathematik, Theorien)

In vielen Erkenntnistheorien werden die unter 1.2.2 dargestell­ten komplexen Opera­tionen der Phantasie, die laufend ganze Bildwelten erzeugt, ständig im Gedächtnis vorhandene raum­zeitliche, plastische Bildkompositionen umstellt, verändert und neu organisiert, überhaupt nicht in der gesamten Tragweite er­kannt und berücksich­tigt. (Die Phantasie ist natürlich nicht nur im Wachen, sondern auch im Traum tätig, was wir hier nicht weiter untersuchen.) Die sinn­liche Erkenntnis wird u.U. als ein einfaches Reiz-Reaktionsverhältnis, als In­put-Outputsystem verstanden. Noch viel schwieriger ist die Erschließung des für die sinnliche Erkenntnis im weite­ren unerlässlichen Anteils "kognitiver" Ope­rationen begrifflicher Art. Hier finden sich  wieder eine Viel­zahl von Ansichten in der Erkenntnistheorie. Einige Schulen meinen, Begriffe stammten ausschließlich aus der sinnlichen Erfah­rung, man lernte eben Sprachen und ihre Bedeutungen. Andere Schulen mei­nen, Begriffe müssten wir schon von vorn­herein (a priori) im Bewusstsein (nach anderer Formulierung im Geist) ha­ben, damit wir überhaupt als Kleinkinder sinnliche Erkenntnis zustandebringen können und überhaupt die Laute der El­tern als Sprache "verstehen" und dann die gesellschaftlich gegebene (z. B. deut­sche) Sprache zu erlernen vermögen. Wir hatten also schon Gedanken, Begriffe, bevor wir die Wörter ei­ner Sprache lernen. (Wir haben auf jeden Fall zwischen dem Gedanken und seiner Darstellung als Zei­chen in einer Sprache zu unterscheiden!) Die nächste Schule meint gar, dass bestimmte, z. B. logische Gedanken, wie FREGE sagt, nicht Erzeugnis unserer seelischen Tätigkeit sind, sondern im Denken nur "gefunden" werden. "Denn der Gedanke, den wir im Pythagoräischen Theorem ha­ben, ist für alle derselbe, und seine Wahrheit ist ganz unabhän­gig davon, ob er von diesem oder jenem Menschen gedacht wird oder nicht. Das Denken ist nicht als Her­vorbringung des Gedankens, sondern als dessen Erfassung anzusehen." (Vgl. auch PENROSE S. 95 + 418.)

1.2.3.1 Systematische Analyse der Erkenntnisbegriffe

Wir versuchen jetzt in möglichst einfachen Formulierungen ganz entscheidende Pro­bleme darzustellen. Es ist schon ein großer Fortschritt zu erkennen, dass wir eine Vielzahl von Be­griffen (C) benützen und einsetzen müssen, um überhaupt eine sinnliche Er­kenntnis zustande zu bringen. Ein noch schwierigeres Unterfangen aber ist es, eine Analyse die­ser Begriffe durchzuführen und sie als ein System darzustellen. Das System von Be­griffen wäre dann auch gleichzeitig das Schema, nach dem wir alles zu erkennen und zu denken hätten. Dieser Versuch macht einen brei­ten Teil der Geschichte der Er­kenntnistheorie aus, und es gab immer wieder neue Be­mühungen, diese Grundge­danken – früher Kategorien genannt – zu sy­stematisieren. Wir erwähnen hier nur ARISTOTELES, KANT und WITTGEN­STEIN im Traktat. Die Begriffssysteme der drei Denker sind sehr unterschied­lich ausgefallen. Auf die Differenzen gehen wir hier aus Platzgründen nicht ein. Wir möchten aber in diesem Zusammenhang auf eine philosophi­sche Frage zu­mindest hinweisen, die nun gestellt werden muss und auch in der Geschichte immer wieder gestellt wurde: Wenn wir Erkenntnis der Außenwelt durch eine Synthese aus Sinneseindrüc­ken (E), Bildkonstruktionen in äußerer und inne­rer Phantasie D(1) und D(2) und Begriffen (C) zustandebrin­gen, von denen ein Teil Grundbegriffe bilden, die in einem Sy­stem erfassbar sind und bei allen Erkenntnissen benützt werden sollen, dann erhebt sich die weitere Frage, woher wir denn wis­sen sollten, ob die Anwendung dieser Grund­begriffe auf alles, was wir denken und erkennen, zu­lässig sei. Können wir uns da nicht auch täuschen? Woher sollen wir denn wis­sen, ob es zu­lässig ist, diese Begriffe auf alles anzuwenden, was wir denken, vor allem auf die Welt außerhalb unser. Ist die Welt denn auch wirklich so gebaut, wie wir sie uns denken? Hat die Welt denn die gleiche Struktur wie das System der Grundgedanken, das uns da von den Philo­sophen vorgeschlagen wird? Diese Frage zu stellen, bedeutet einen besonderen Schritt in der Erkenntnis­theorie. Sie nicht zu stellen, bedeutet umgekehrt, dem menschlichen Erkennt­nisvermögen eine Grenze zu setzen, die eigentlich unzulässig ist. Da wir ein­gangs ankündigten, die Frage der Grenzen der MI zu untersuchen, gelangen wir hier an eine entschei­dende Stelle. Wird die Zulässigkeit dieser Frage geleugnet, er­folgt bereits eine für die ge­samte Entwick­lung der Erkenntnistheorie und im weiteren für das Verständnis der Erkenntnisgrenzen der MI relevante BEGREN­ZUNG UND EINZÄUNUNG mit schwerwie­genden Folgen. Diese Grenz­ziehung erfolgt etwa damit, dass man sagt: "Menschliche Er­kenntnis ist auf den Aufbau von Theorien zu beschränken, die auf Begriffe der Theorie C(T), Logik und Mathe­matik sowie auf Beobachtungen zu be­schränken sind. Darüber hinausge­hende Erkenntnisse sind sinnvoll nicht zu gewin­nen. Die for­male Lo­gik ist die nicht über­schreitbare Grundlage des Auf­baus von Erkenntnis, sozusagen die innerste Grundlage der MI." Mit dieser Begrenzung hat sich das menschliche Erkenntnis­streben nie zufrie­den ge­geben. Die Überschreitung dieser Grenze wirft also die Frage auf, ob jen­seits des Menschen und der "Welt" ein absolutes und unendliches Grundwesen existiert, in/unter dem sowohl der Mensch als auch die Welt enthalten sind. Gibt es ein solches Grundwesen, ergibt sich die weitere Frage, inwieweit es dem Menschen erkennbar ist. Denn wenn eine solche menschliche Erkenntnis des Grundwesens möglich ist, dann müsste vom Menschen auch erkannt werden können, wie alles an oder in/unter dem unendlichen und unbedingten Grundwe­sen enthalten ist. Unter der Vorausset­zung, dass dies möglich ist, ergeben sich entscheidende Folgerungen:(1)   Wahr erkennen wir nur dann, wenn der Bau unseres Den­kens so gebaut ist, wie alles in/unter dem Grundwesen enthalten und gebaut ist. Also der Bau des Den­kens (Logik) muss so sein wie der Bau der Welt, des Univer­sums, des Weltalls in/unter dem unendlichen Grundwe­sen.(2)   Ist eine solche neue Logik (synthetische Logik, SL) auf­findbar, dann ist zu prü­fen, inwieweit alle bisherigen Lo­giken in der Geschichte der Erkenntnis­theorie Mängel be­sitzen, "zu eng" sind oder gar bestimmte Teile derselben überhaupt nicht besitzen.(3)   Mit dem Vorhandensein einer solchen Logik würde sich aber auch der Auf­bau der Wissenschaft, vor allem auch der Naturwissenschaft, entscheidend verändern.Hier sei zur Klarstellung für den Leser auf einen sehr wichtigen Unterschied in der Art der logischen Systeme hingewiesen. Die einen Denker sagen: Der Bau eines logi­schen Systems muss sich nach dem Inhalt dessen richten, was wir den­ken  – In­haltslogik, etwa bei HEGEL –, die anderen meinen, die Logik sei aus bestimmten, ihr eigentümlichen Gesetzen so aufbaubar, dass das System – unab­hängig vom Inhalt, auf den die logi­schen Gesetze und Regeln später angewendet werden – rein der Form nach aufgebaut werden könnte. (Systeme der for­malen Logik, über de­ren Entwicklung J.M.BOCHENSKI eine gründliche und subtile Darstellung gibt; Alber Verlag, 1970.)Die hier gemeinte Logik, die sich aus der GRUNDWISSEN­SCHAFT ergibt, ist IN­HALTSLOGIK und FORMALE LO­GIK in völliger Übereinstimmung und Dec­kung. Ist es nun möglich, den Weg zu beschreiten, den wir hier als WENDE ZUR GRUNDWISSENSCHAFT (W_Gr) bezeichnen wollen? Eine Reihe von Philoso­phen hat es behauptet. Auch dieser Typ von Systemen hat eine Entwicklung durchge­macht. Die Inhaltslogik HEGELs hat weitreichende geschichtliche Be­deutung er­langt. Ein anderes System erweist sich – zumindest nach unserer An­sicht – als bahnbre­chend für die weitere Ent­wicklung der Wissenschaft dieser Mensch­heit: die Grundwis­senschaft des bisher eher unbeachtet gebliebenen Philoso­phen KRAUSE. Diese Grundwis­senschaft ist in den von mir 1981 neu herausgege­benen "Vorlesungen über das System der Philosophie" enthalten, die sich daraus er­gebende Logik im Werk "Vorlesungen über Synthetische Logik". Die Grundlagen der Mathematik sind ebenfalls in der GRUNDWISSEN­SCHAFT und in einem Aufsatz enthalten, der im Buch Pflegerl: "Die Vollendete Kunst" neuerdings abge­druckt ist. Im hier begrenzten Rahmen wäre es unmöglich, diese Lehren darzustellen. Wir wer­den aber unter Berücksichtigung dieser neuen Grundwissenschaft, den Ver­such un­ternehmen, an einem BEISPIEL, das jedem Leser leicht einsichtig sein wird, zu zei­gen, worin die bahnbrechenden Neuerungen dieser Lehren für Logik und Mathema­tik be­stehen. Bereits an diesem, relativ ein­geschränkten Beispiel lassen sich nämlich die Grundzüge der neuen Logik (SL) und jene Axiome zei­gen, welche in der Lage sind, die Grundlagenkrise der modernen Mathematik und damit auch der mathema­tischen Logik zu beheben. Festgehalten sei aber, dass eine kritische Auseinanderset­zung mit der Grundwis­senschaft nicht um­hinkäme, diese selbst und die SL gründlich durch­zudenken.

1.2.3.1.1 Das Universum der geraden Linie o

In der Mathematik sind Gedankenmodelle beliebt. (Man über­legt etwa, welche Geo­metrie Lebewesen hätten, die nur aus zwei Dimensionen bestehen und auf einer Ku­gel leben.)In unserem Gedankenexperiment wollen wir annehmen, es lebe irgendwo eine Ge­sellschaft von Menschen, das Volk der Kari­donier, dessen Universum nur aus einer unendlich langen, ge­raden Linie besteht. Generationen von Forschern analysieren dieselbe und stellen Überlegungen an, wie diese Linie richtig zu er­kennen sei, welche Logik sich aus den Inhalten dieser Er­forschung ergebe. Sie fragen also: Wie muss der Bau unserer Logik sein, damit wir die Linie so den­ken, wie es ihrem Inhalt, ihrem Bau entspricht. Hier das Ergebnis: Wichtig ist bereits einleitend zu beachten, dass die deutsche Umgangssprache nicht ausreicht, um die hier entwickelten Er­kenntnisse genau zu bezeichnen. Es müssen daher einige neue, klarere Bezeichnungen für das Erkannte, für das Gedachte ein­geführt werden (z. B. "Or" für das Ungegenheit­lich/Ganze/Eine, "ant" für das Gegen­heitliche, "mäl" für das Vereinte, "Ab" für die Beziehung des Höheren zum Niederen, "Neb" für die Beziehung von Nebengliedern usw.). Da die hier deduzierten, abgeleite­ten Begriffe im System (LO) eine andere Bedeu­tung haben, als in der bisherigen Umgangssprache und den bisherigen Wissen­schaftssprachen, werden sie in der Axiomatisierung (LO) in einer besonderen Schrift (Lucida Sans) ge­schrieben. Umgekehrt wird hier aber auch dazu ange­regt, bisher überhaupt nicht gründlich genug Ge­dachtes erst einmal überhaupt zu denken.

(LO 1) Was die Linie o AN sich ist

"AN" einem Wesentlichen ist, was von ihm ganz, durchaus gilt. "IN" einem We­sentlichen ist dasjenige Wesentliche, welches von ersterem ein Teil ist, und Gleichar­tiges des ersteren außer sich hat. Betrachtet wird bei der Linie o in (LO 1), was sie AN sich ist, also noch nicht, inwie­weit sie vielleicht auch Teile usw. hat.(LO 1.1) AN der Linie o wird die Wesenheit go (in der FIGUR 2 go, gu, gi, ge usw.) er­kannt. An der Wesenheit die Einheit. Dass die Linie im weiteren (LO 1.2) und (LO 1.3) auch Zweiheit, Mehrheit, Vielheit,

Vereinheit von mehreren Teilen usw. ist und hat, wird hier noch nicht erkannt. Die Einheit, die hier er­kannt wird, ist eine ungeglie­derte, allen Teilheiten und Viel­heiten "IN" der Linie übergeordnete Einheit, die wir der Ge­nauigkeit wegen als Or­Einheit (go) bezeichnen können.

(LO 1.2) AN der Wesenheiteinheit go der Linie werden die Selbheit (gi) und die Ganzheit (ge) erkannt. Die Selbheit be­zeichnet man üblicherweise als Absolutheit und die Ganzheit als Unendlichkeit. Die Linie ist AN sich Eine, absolut und un­endlich. Das Wort "Ganzheit" meint hier nicht eine Summe von Elementen, die zu einer Ganzheit zusammengefasst sind. (Diese finden sich erst in (LO 1.2 und LO 1.3.) Die Linie o ist IN sich auch Summen von Teilen usw. Aber als Linie o ist diese Ver­ein–Ganzheit von Teilen noch nicht ersichtlich oder erkennbar. Diese Or–Ganzeit oder unendliche Ganz­heit ist ein "über"geordneter Begriff. Das Wort "Selbheit" oder Absolutheit" der Linie o meint, dass sie an sich ist, ohne ir­gend ein Verhältnis nach außen. (Dies stimmt auch in unserem Modell, da es bei den Karidoniern au­ßer der Linie o ja nichts gibt.)Wesenheiteinheit (go), Selbheit (gi) und Ganzheit (go) stehen in der Gliederung der FIGUR 2 zueinander. Für die Gliederung der Mathematik sind go, gi und ge die Grundaxiome. Für die Lehre von Gegensatz, Negation, positiven und negativen Zahlen sind es die Ablei­tungen  IN go, für die Lehre von den Verhältnissen sind es die Ableitungen IN gi und für die Ganzheitslehre die Ab­leitungen  IN ge. Go und ge sind auch mitein­ander ver­eint und mit go als gu.

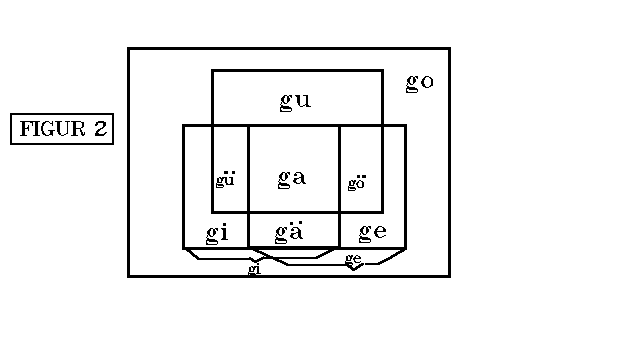
(LO 1.2.1) Wie ist die Wesenheit-Einheit (go) und wie sind im weiteren gi, ge und alle Verbindungen der Linie o in FIGUR 2? Die FORM der Wesenheit go ist Satzheit do. Die Linie o ist das eine Gesetzte, Positive. Hier An der Linie o gibt es noch keine Nega­tion, kei­nen Gegen–Satz usw. Wir bezeichnen diese Satz­heit als Or-Satz­heit. Die Form der Selbheit gi ist Richt­heit di oder Bezugheit (Relationalität), aber auch hier gibt es nur die Eine Richtheit ohne noch ein Hin und Her oder son­stige ein­zelne Richtungen zu un­terscheiden, also Or-Richtheit. Die Form der Ganzheit ge ist Fassheit de ("um"fangen, befas­sen). AN der unendlichen, ganzen Linie wird noch nicht ein Um-fas­sen endli­cher Ganzer erkannt, sondern dieses Fassen der Or-Ganzheit hat keine Endlichkeit (FIGUR 3).

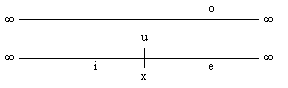
(LO 2)  Was die Linie o IN sich ist

Die Linie o ist IN sich gemäß der obigen Zeichnung Gegenlinie und Vereinlinie nach INNEN, so dass die Linie IN sich zwei ihr als o untergeordnete und IN ihr selbst als ganzer selber Linie nebengegenheitliche Linien i und e ist, wel­che AN sich gleichwe­sentlich und sich darin neben-gegenheitlich sind, dass die eine von bei­den ist, was die andere nicht ist und umgekehrt. Die Li­nie o aber, sofern sie ÜBER sich selbst als die beiden neben­gegenheitlichen entgegengesetzten Li­nien i und e ist, ist die Urlinie u, von i und e unterschieden, und in­soweit ist die Linie o in sich eine doppelgliedrige AB-Gegen­linie. Die Linie ist als u auch vereint mit den beiden Gegenli­nien i und e. Die beiden Ne­ben-Gegenlinien sind eben­falls mit­einander vereint.

(LO 2.1) IN der Linie o in der ersten Gliederung sind nur 2 Li­nien, die durch den Punkt X voneinander getrennt sind. Es gibt das Erste und das Zweite, das Zweite ist das Andere des Ersten. Das Erste ist, was das Zweite nicht ist und umge­kehrt. Beide sind einander nebenentgegengesetzt, ne­bengegenheitlich, andererseits ist aber die Entgegenge­setztheit der beiden gegen die Linie u eine Ab-gegenheit. Die Gegenheit der beiden Glie­der gegen u ist also eine andere als die Gegenheit der beiden i und e gegenein­ander. Die Linie o ist IN sich beide. Man kann also nicht sagen, das Eine ist die Linie o und das Andere sind die beiden Linien i und e. sondern es ist zu sagen: Die Linie o ist In sich sowohl das Eine als auch das An­dere. Unrichtig ist aber zu sagen: Die Linie o ist beide. Dar­aus ergibt sich, dass die innere Gegenheit in der Linie o zwei Glieder hat. Es ist unmöglich anzunehmen, dass die in­nere Gegenheit nur ein Glied hätte. Dadurch dass die eine der beiden Linien i nicht ist, was die andere Linie e ist, wird von der Li­nie o überhaupt nichts verneint. Weiterhin ist zu beachten, dass die Linie o, soweit sie ÜBER i und e ist, und erst in dieser Hinsicht eine Beziehung nach innen hat, in (LO 1) aber, AN der Or-Linie o solche Beziehungen nicht gegeben sind ( Es sei denn, man meint alle Be­ziehungen, die wir in (LO 1) darleg­ten, diese Beziehungen sind Aber AN-Beziehungen.)  

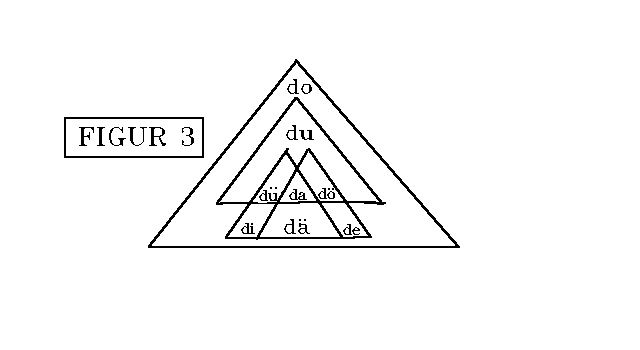
(LO 2.2.) Die in (LO 1.2) angeführten Begriffe der Wesenheit und ihrer AN-Gliederung, also Wesenheiteinheit, Selbheit (LO 2.2) Die in (LO 1.2) angeführten Begriffe der Wesenheit go und ihrer AN-Gliede­rung

n     also Wesenheiteinheit, Selbeit und Ganzheit (FIGUR 2) - erfah­ren bei der Gliede­rung der Linie o IN (LO 2) durch Linie u und die beiden Linien i und e ebenfalls eine Ab-Gegen-, Neben-Ge­gen- und Vereingliederung, die folgend dar­stellbar ist:

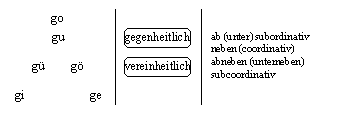
(LO 2.2.1) Die Wesenheit go, der unendlichen unbedingten Linie o erfährt an den beiden Linien i und e eine Veränderung. Die Neben-Gegen-Wesenheit der beiden Li­nien ist ihre Art­heit (Art, Qualität). In der Linie o ist zuerst einmal eine nur zwei­gliedrige Artheit: der qualitative Unterschied zwischen i und e.

(LO 2.2.2) Für die beiden Nebengegen-Glieder i und e ergibt sich als Gegenheit der Selbheit (gi) die Verhaltheit, das Verhält­nis. Sie stehen zueinander in einem Neben-Ver­hältnis, zur Linie u in einem Über-Unterverhältnis usw. AN der Linie o in (LO 1) gibt es keine Gegen-Verhält­nisse, sondern die Eine Selbheit, als Or-Selbheit. i verhält sich zu e in bestimmter Weise. Das Gegenselbe steht sich als ein Anderes wechsel­seitig entge­gen, eines ist des anderen Objekt.

(LO 2.2.3) Für die beiden Neben-Gegenglieder i und e ergibt sich als Gegenheit der Ganzheit (Or-Ganzheit der Linie o) die Teilheit. Das Gegenganze ist Teilheit. Die Linie o ist IN sich zwei und nur zwei Teile i und e. Hier ist auch die höchste Grund­lage des Mengen­begriffes gegeben. Man kann nicht sagen: die Linie o ist eine Menge, weil AN der Li­nie überhaupt keine Teilheit ist, wohl aber die Linie o ist IN sich in dieser er­sten Ge­genheit zwei und nur zwei Teile (Elemente). Wir unterschei­den aber die Ab-Teilung von der Neben-Teilung. Denn die untergegenheitlichen Teile nennt man Unter-Teile, (Ab-Ant-Ganze). In der Vereini­gung ergibt sich das Verein­ganze der Teile, die Erste Summen­bildung von i und e

(LO 2.3). Auch hinsichtlich des Wie der Wesenheit usw. hin­sichtlich der Begriffe der Formheit do usw. ergeben sich für die gegenheitlichen Linie i und e neue Be­stimmungen.

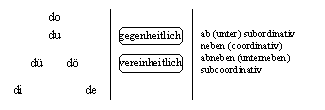
Unter (LO 1.2.1) fanden wir, dass die Linie o Satzheit do hat. Hinsichtlich der Gliede­rung o, i, e, usw. ergibt sich hier Ge­gen-Satzheit und zwar wiederum Neben-Gegen­satz zwischen i und e, Ab-Gegensatzheit zwischen u und i usw. Die Gegensatzheit ist die Bestimmtheit. Bestimmtheit ist also eine Teilwesenheit an der Satzheit als Gegensatz­heit. i ist also gegen e bestimmt, aber auch u bestimmt e und i usw. Diese Gegen­satzheit hat selbst auch eine Form. Die Or-Satzheit ist der Form nach ganz Jaheit, ohne Neinheit, also Or-Jaheit. Diese Jaheit ist nun selbst wie­derum gegliedert

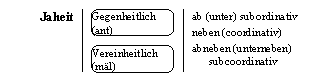
Statt der Or-Jaheit kann man sagen, die unendliche und unbe­dingte Positivität. Was die Gegen-Jaheit betrifft, so ist diese zugleich Gegen-Neinheit, entgegengesetzte Vernein­heit (oppositive Ne­gativität). Das Nein oder Nicht wird daher nur hier erkannt. Die Gegennein­heit ist nur an der Gegenjaheit. Da­durch dass i be­stimmt ist als das Eine von zwei Wesentlichen, ist es auch zugleich bestimmt als nicht sein Anderes, sein Ge­genheitliches, hier also e ist von ihm verneint. Das Nein ist also nur in einer Be­ziehung gegen ein Anderes. Durch die gegensei­tige Teilverneiung i gegen e und umgekehrt, wird von der Unendlichen und unbe­dingten Li­nie o überhaupt nichts verneint. Hinsicht­lich der Li­nie o ist das Nicht nicht. Die Be­stimmtheit i gegen e besteht darin, dass es e aus­schließt. Hier liegt die Grundlage der Wörter ja, nein, Nichts, des logischen „ist nicht“. Zu beachten sind na­türlich auch die Ge­genjaheiten von der Li­nie u gegen i bzw. e (Unter-Gegen-Verneinung oder Ab-Ant-Verneinung).

(LO 2.3.1) Auch die Satz-Einheit, an der Linie o unendliche und unbedingte Einheit der Satzheit (oder Zahleinheit), ist hier gegenheitlich zu finden als:

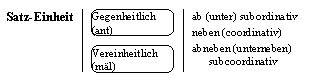
also Satz-Gegeneinheit, Satz-Vereinheit. Für die Zahl-Gegeneinheit wird das Wort Vielheit oder Mehrheit benützt. Zu beachten ist aber, dass hier noch keine Vielheit ge­geben ist, die mehr als Zweiheit wäre (Gegeneinheit). Statt der Vereinzahlheit sagt man All­heit, Totalität, die aber hier nur aus zwei vereinten Gegen-Glie­dern besteht. Von der Linie o gilt unbedingte und unendliche Zahleinheit, keine Vielheit, oder Mehrheit, keine Allheit. Die Linie o ist IN/UNTER sich die Vielheit und das Viele, die All­heit und das All oder die Totali­tät, das Universum aller Glieder in sich. Jede ur­sprüngliche Vielheit in der Linie o ist eine Zwei­heit, und jede Vereinzahlheit ur­sprünglich eine vereinte Zweiheit, da der Gegen­satz, oder die nach Ja und Nein be­stimmte Gegen­heit nur zweigliedrig ist. Die unbe­stimmte Vielheit oder Viel­zahligkeit ist hier noch nicht gegeben, z.B. die unendliche Viel­zahligkeit 1,2,3,4,5, usw.

Hier liegen die Grundlagen der Zahlentheorie: die oberste Zahl ist die unendli­che, unbedingte Eins (o). In ihr sind die bei­den ge­genheitlichen Zahlen i und e, die ebenfalls noch unend­lich sind, aber gegeneinander begrenzt durch X. Sie sind nicht mehr ab­solut, sondern gegeneinander und gegen u relativ. Hier liegen die Grundlagen der widerspruchs­freien Mengenlehre. Denn die beiden ersten „Mengen", INNE­REN Ele­mente, von o sind i und e, beide selbst noch unendlich, aber bereits re­lativ.

(LO 2.3.1.1) Die Form der Satzeinheit oder Zahleinheit ist die unendliche, unbe­dingte Jaheit. Die Jaheit ist dann selbst wie­derum gegliedert wie unter (LO 2.3). Daraus er­gibt sich die Ja­heit und Neinheit der Zahlheit, hier aber erst für die beiden Teile i und e. Hier findet sich die Grundlage der mathemati­schen Lehre von den Zahlen und Gegenzahlen (den positi­ven und negativen Zahlen).

(LO 2.3.1.2) Auch die Richtheit di (als Form der Selbheit in LO 1.2.1) erfährt hier weitere Bestimmung:

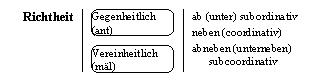
Hier wird die Gegenrichtheit erkannt. Und zwar haben i und e nebengegenheit­liche Richtheit. i „fängt“ bei X an und „geht in die eine Richtung", e „fängt“ bei X an und „geht in die andere Richtung“. Weiters ist die Richtung von u nach i und e und um­gekehrt von i nach u usw. zu erkennen. Anstatt Richtheit sagt man gewöhnlich Di­mension, Erstreckung. Der Begriff der Richtheit ist für die Ausbil­dung der Mathematik wichtig, bisher aber ungenau erkannt und entwickelt. Hier ist zu unterscheiden: die Eine Ganze Richtheit (Or-Richtheit di) der Linie o; die Ne­ben-Gegen­richtheit an den Teilgan­zen i und e und andererseits die Ab-Gegenrichtheit u gegen i und e usw. Hier hat der Be­griff der Richtheit noch nichts mit Zeit und Bewegung zu tun. (In der Umgangsspra­che wird Richtung ausgedrückt durch: hin und her, auf und ab, hinüber und her­über.)

(LO 2.3.1.3) Auch die eine selbe ganze Fassheit de, als Form der Ganzheit er­fährt hier Bestimmung.

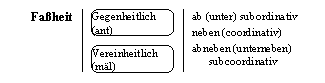
Die Linie o hat „ungeteilte“ ganze Fassheit (Or-Fassheit), die beiden inneren Teile i und e haben Neben-Gegenfassheit, u hat ge­gen i und e Ab-Gegen-Fassheit, schließlich erkennen wir alle Ver­einfassheiten. Auch hier kann man sagen, dass die Linie o ganze Fass-Jaheit hat, dass aber von i und e neben-wechselseitig Fassjaheit und Fassneinheit gilt. Denn i fasst das, was e nicht fasst und umgekehrt. Daraus er­gibt sich das In-Sein und Außensein. e ist außer i und i ist außer e.

(LO 2.3.1.3.1) An dieser Stelle müssen wir noch genauer fra­gen: Wie ist die FORM dieses In-und Außensein? Die Form dieses einander In- und Außenseins ist die Grenz­heit. Das sieht man leicht indem man sagt: X ist die Grenze von i und e. Dort wo die Inbefassung von i aufhört, an der Grenze X, da fängt die Inbefas­sung von e an. Grenz­heit, Grenze ist also die Form des Ge­genfassigen. Es ist also deutlich, daß An der Linie o keine Grenze ist, sondern dass erst in der ersten In-Teilung der­selben, an i und e die Grenzheit als X gegeben und erkannt wird. i und e haben daher eine gemeinsame Grenze. Die Grenze X ist weder i noch e, sie ist ihre gemein­same Grenze.

(LO 2.3.1.3.2) Fragen wir nun, was ist IN dem, was da inge­fasst, eingefasst wird. Der Inhalt des Infassigen wird als groß oder Großheit bezeichnet. Damit Größe da sein kann, muß etwas innerhalb bestimmter Grenzheit bejahig befasst sein. Der Be­griff der Groß­heit ist wiederum für die Mathematik grundlegend. Man hat daher die Ma­thematik oft irrtümlich auf die Größen­lehre beschränkt. Hier wird aber gezeigt, dass die Mathe­matik viel mehr umfasst, und dass der Begriff der Groß­heit bisher auch nicht richtig erkannt wurde.

Betrachten wir das inbegrenzte Große, so erscheint die Grenze desselben als dessen Ende, als Endheit, oder umgekehrt als An­fang. Hier erkennen wir die Begriffe Endheit, Endlich­keit, und Un-Endlichkeit. Die Endlichkeit ist eine Bestim­mung der Grenzheit, die Grenzheit wieder eine Bestimmung der Gegen­faßheit an der Großheit und mithin daher eine Be­stimmung der Ganzheit als Gegen­ganzheit. Daraus zeigt sich, daß der Begriff der Endlichkeit nicht richtig gefun­den wird, ohne die Begriffe der einen, sel­ben, ganzen Richtheit (di), der Faßheit (de) und der Ganzheit (ge). Von der Linie o kann nicht gesagt werden, daß sie an sich endlich ist, oder Grenze hat, sondern nur, dass sie ganz (organz) ist und in ihrer Ganzheit auch alle Endlichkeit und Grenzheit des Gegen­ganzen in sich befasst.

(LO 3) In der dritten Erkenntnis fassen wir zusammen, was bisher erkannt wurde, also was die Linie o AN und IN sich ist.

Es gilt: Die Linie o ist AN sich und IN sich ein Organismus, heute würde man auch sagen eine Struktur. Die An-Gliederung und die Ingliederung wurden un­ter (LO 1 und LO 2) darge­stellt.

(LO 3.1) Dieser bisher dargestellte Gliedbau (Organismus, Struktur) der Linie o ist „voll"ständig. Hier ergibt sich die erste Erkenntnis hinsichtlich der Begriffe ALL-heit, Totalitiät. Diese Allheit ist aber nicht irgendeine unbestimmte ver­schwommene, sondern die Gliederung ist deutlich bestimmt.

(LO 3.1.1) Aus dieser Gliederung ergibt sich auch, dass die Ge­genheit nur zwei­gliedrig ist, denn es gibt keine anderen inneren Glieder der Linie o als i und e, und deren Ja­heit und Gegenja­heit (Neinheit). Natürlich gibt es auch „noch end­lichere“ Linie in o, aber das wird sich erst im folgenden ergeben.

(LO 3.1.2) Für diesen gegliederten Organismus gilt auch, dass alle hier entwic­kelten Begriffe aufeinander anzuwenden sind. So hat z.B. die Ganzheit (ge) auch Wesenheit, Selbheit und Gegen­selbheit, also Verhaltheit, Ganzheit, sie hat eine be­stimmte Form oder ist in bestimmter Grenzheit, gegenüber der Selbheit, usw. Wenn also derjenige Teil der Mathematik der sich mit Größen beschäftigt, voll ausgebildet werden soll, dann muss an der unendlichen und nach innen ab­soluten Ganzheit (hier Or-Ganzheit der Linie o) begonnen werden, was bisher nicht geschehen ist. Ein anderer Zweig der Mathematik ergibt sich aber aus der Selbheit (gi) und Gegenselbheit (Verhaltheit, Verhältnis), wenn dieser Begriff nach allen anderen Begriffen durchbestimmt wird (z.B. die Lehre von den Pro­portionen usw.).

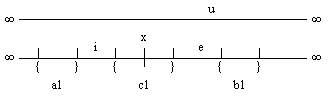
(LO 4.1) Jeder der beiden Teile i und e in der Linie o (und auch die Vereinigung der beiden) ist selbst wiederum AN und IN sich Struktur, Organismus gemäß der Struk­tur (LO 1-3), also hat selbst wieder eine der Linie o ähnliche Struktur.

Es gilt: Wie sich die Linie o zu u, i und e und deren Gegen­heiten und Vereinhei­ten verhält, so verhält sich wiederum i zu dem, was es IN sich ist, usw...

(LO 4.1.1) Die Form dieses Ähnlichkeitsverhältnisses ist die Stufung, Abstufung (Stufheit), wo­bei sich das unter (LO 2.3.1.3) dargestellte Insein und Außensein nach innen fort­setzt.

(LO 4.1.2) Fahren wir nun mit der inneren Gliederung von i und e und deren Verei­nigung fort, so ergeben sich in i unend­lich viele Linien gemäß a1, in e unendlich viele Li­nien wie b1 und in der Vereinigung von i und e unendlich viele Linien wie c1. Analysie­ren wir die Ganz­heit, Großheit, Grenzheit und Endlichkeit (LO 2.3) dieser Linien a1, b1, c1, so fällt auf, dass sie zum Unter­schied von den Linien i und e „auf bei­den Seiten endlich sind“, beidseitig begrenzt sind, sie sind also ganz endlich, oder unend­lich-endlich. i und e sind also in sich unendlich endliche Glieder. Ein solches Glied der Linie o nennt man nun individuell, parti­kular. Wichtig ist zu erkennen, dass sich die Art der Endlichkeit von i einerseits und a1 andererseits unterscheiden. Die Glieder i und z.B. a1 gehören ver­schiedenen Stufen der Grenzheit, Begren­zung, verschie­denen Grenzheitsstufen an. Die Er­kenntnis dieses Unter­schiedes in der Grenzheitsstufe von Elementen in einem un­endlichen Ganzen ist ent­scheidend, um die Antinomien der bis­herigen Mengenlehre zu vermeiden.

(LO 4.1.3) Frage: Hat diese Gliederung der Linie o nach innen ein Ende? Ja! Und zwar: Die Linie o ist beidseitig unendlich. Genauer gesagt: sie hat unendli­che Or-Richtheit. Die Linien i und e gehö­ren noch der gleichen Grenzheitsstufe an, sie sind auch noch unendlich, haben aber gegeneinander die Grenze X, sind nur mehr einsei­tig unendlich (endlich-unendlich). Die Glieder a1, b1, c1, sind beidseitig endlich, sind also in der Stu­fung der Grenzheit noch weiter innen. Teilt man jedoch a1 weiter in 3 Teile, so erhält man der Artheit nach keinen neuen Typ von Li­nien, weil 1/3 von a1 wiederum eine beidseitig be­grenzte Linie ist. Die Grenzheitsstufe der Linientypen a1, b1, usw. ist also die letzte innere Grenzheitsstufe der Linie o. Hier ist das Ende der Endlichkeit (unterste Grenz­heit; Grenze der Grenze).

(LO 4.1.4) An diesen unendlich endlichen Gliedern (Elementen) in/unter o ist nun in zweifacher Hinsicht Unend­lichkeit.

1.     In den Gliedern i, e und ihrer Vereinigung gibt es jeweils unendlich viele unend­lich endliche Elemente (a1..,b1..,c1..).

2.     Jedes unendlich endliche Glied a1, usw. ist selbst weiter unendlich teilbar und bestimmbar.

(LO 4.1.5) Das Endliche, Bestimmte oder Individuelle jeder Art und Stufe ist also nicht isoliert, gleichsam losgetrennt von dem, was neben und außer, über ihm ist (z.B. a1 von o), es ist in/unter seinem höheren Ganzen und mit ihm ver­eint, wie auch mit den Nebengliedern.

(LO 4.1.5.1) Aus den bisherigen inneren Gliederungen der Li­nie o ergeben sich nun folgende weitere axiomatische Folge­rungen:

Die Stufung der Grenzheit und die Großheit sind nun mit der Selbheit und der Ge­gen-Selbheit, also der Verhaltheit verbun­den (vereint). Die allgemeine Lehre von der Verhaltheit (von den Verhältnissen) begreift in sich Verhältnis, Verhältnis­gleichheit (Analogie, Proportion), Verhältnis-Un­gleichheit (Disproportion), Verhältnisreihe (Progression), nach gleichen oder ungleichen Verhältnissen; die ersten Reihen sind Gleichver­haltreihen oder Verhaltstuf­reihen (Potenzreihen). Hinsichtlich der Verhält­nisgleichheit zeigt die reine Selbheitlehre zwei Grund­operationen: zu einen ge­gebenen Musterverhalte und einem ge­gebenen Hinterglied das gleichverhaltige Vorderglied zu fin­den; oder: zu ei­nem ge­gebenen Vorderglied das gleichverhal­tige Hinterglied zu fin­den. Auf die Ganzheit angewandt sind dies das Multiplizie­ren (Vorgliedbilden) und Dividieren (Nachgliedbilden).

(LO 4.1.5.2) Ferner entsteht hier das grenzheitsstufliche Ver­hältnis, also das Ver­hältnis von Ganzen, die zu verschiedenen Stufen der Grenzheit gehören (z.B. Linie i zu b1 usw.), als auch grenzheitsstufliche Verhältnisgleichheit, Verhältnis-Un­gleichheit und Verhältnis­reihe. Auch die analogen Axiome hin­sichtlich der Verhält­nisse von solchen Ganzen, die innerhalb einer und der selben Stufe der Grenzheit enthal­ten sind.

(LO 4.1.5.3) Hier ergeben sich nun zwei in der bisherigen Ma­thematik und Mengen­lehre nicht beachtete wichtige Folgerun­gen.:

Jede selbganzwesenliche also unendliche und ansich unbe­dingte Einheit jeder Art und Stufe (hier die Linie o) ist in/unter sich unendlich viele Einheiten der nächstnie­deren Grenz­heitsstufe (hier a1, b1, usw; beachte i und e sind von der glei­chen Grenz­heitsstufe, wie die Linie o selbst!!) und so ferner bis zur unter­sten Grundstufe (die hier mit der beidseitig be­grenzten Linie gegeben ist). Diese Grundstufe ist nach allen Richtheiten (Strecken, Dimensionen) endlich, und be­steht selbst wiederum aus un­endlich vielen Einheiten dieser unter­sten Stufe (a1 kann man weiter unendlich tei­len). Jede jedstufige unendliche Ein­heit besteht aus unendlich vielen unendlich end­lichen Einheiten der untersten Stufe.

(LO 4.1.5.3.1) Wir können uns auch ein ähnliches Volk wie die Karidonier vor­stellen, welches als Kosmos nicht nur eine Linie o sondern eine Fläche besitzt, welche nach den in unserem Arti­kel PC News 3/91; 2.2 erwähnten Grundsätzen gegliedert ist. Da zeigt sich, daß die Fläche in sich 4 Grenzheitsstufen hat, wo­bei erst die 4.Stufe un­endlich endliche Flächen als unterste Stufe ergibt.

(LO 4.1.5.4) Hier zeigt sich auch der Grundbegriff der un­endlichen Vielheit und darin der unbe­stimmten Vielheit oder der un­endlichen und darin der unbestimm­ten Zahlheit, wobei ein Un­endlich-Gan­zes des Gleicharti­gen (hier der Linie o) vorausge­setzt wird, worin inner­halb voll­endet bestimmter Grenze, die endliche Einheit der Unendlich­keit des Gan­zen wegen, will­kürlich angenommen wird.

(LO 4.1.5.4.1) Hierauf beruht die mathematische Vorausset­zung, dass die Zahlen­reihe 1,2,3,.. und so fort unendlich ist und dass auch wiederum an jeder Zahl die ganze Zah­lenreihe darstellbar ist, durch Zweiteilung, Dreiteilung, Vierteilung usw. ohne Ende. Diese hier bewiesene, unendliche und unbestimmte Vielheit, als Grunda­xiom der allgemei­nen Zahlheitlehre (Arithmetik und Analysis) ist wiederum eine doppelte. Einmal die unendliche Artvielheit oder Artzahlheit von Ein­heiten, welche artver­schieden sind, oder die Zahlheit der dis­kreten Zahlen. (Dies ergibt sich aus dem obi­gen Satz LO 4.1.5.3)

Hier zeigt sich aber zum anderen auch die unendliche stetige Zahlheit, oder Stetzahlheit an Einheiten, welche in ih­rem stetigen Ganzen selbst binnen bestimmbarer Grenze ste­tig und unend­lich teilbar sind. Dies ergibt sich aus: Alles Stetige, Wesenheit­gleiche ist in sich unendlich bestimmbar und teilbar. Die Lehre von der Artzahlheit ist übri­gens von der Stetzahlheit zu unter­scheiden.

(LO 4.1.5.4.2) Im weiteren ergibt sich hieraus das Axiom der stetigen Großheit, und der ste­tigen Größen: unendliche Teilbar­keit, unendliche Vielmaligkeit jedes Endlichen in sei­nem Un­endlichen der nächsthöheren Stufe; die Gegenricht­heit hinsicht­lich der Richt­heit (Strecke, Dimension), das ist die Lehre von den gegen­richtheitlichen Größen, den positi­ven und negativen Grö­ßen. Ferner die Axiome der Stet­großheit und der Stetgrößen nach der SELBHEIT und der VERHALTHEIT. Denn es ist eine Größe entweder eine selbheitliche Größe (Selbgröße; ab­solute Größe) oder eine ver­haltliche Größe (gegenselbheitliche Größe), Verhaltgröße, re­lative Größe, welche hinsichtlich der mit ihr verglichenen Größe groß oder klein ist. Die Größever­haltheit ist selbst wiederum eine der Gegenselbheit (ein arith­metisches Verhält­nis oder Restverhältnis) oder eine der Verein­selbheit, darun­ter auch der Vielheit( ein sogenanntes geometri­sches Verhält­nis). Das gleiche gilt von der Verhaltheit hin­sichtlich der Stetgroß­heit.

(LO 4.1.5.4.3) Alle Größen der selben Grenzheitsstufe (hier die Linien a1, bn, c5.. usw.) stehen zu einer jeden beliebigen Größe der gleichen Grenzheitsstufe in einem bestimmten Grö­ßenverhältnis, welche letztere, wenn sie das bestim­mende Glied jedes Verhältnisses ist, die Grundeinheit oder absolute Ein­heit ge­nannt wird. (z. B. Ver­hältnis 1 zu 3 oder 3 zu 1 usw.) Je­des Verhältnis der Un­gleichheit ist diesseits oder jenseits des Ver­hältnisses 1..1, und zwar entweder eines der größeren Un­gleichheit z.B. 3 zu 1 oder der kleineren Ungleichheit z.B. 1 zu 3. (vgl. auch vorne unter LO 4.1.5.1) die Grundoperationen des Multiplizie­rens und Dividierens).

(LO 4.1.5.4.4) Rein nach der Grundwesenheit der Selbheit sind an dem Stet­großen folgende Operationen gegeben: Addition und Subtraktion, indem entwe­der aus den Teilen das Teilganze oder aus einem oder mehreren Teilen des Teil­ganzen der an­dere Teil (der Rest) bestimmt wird.

(LO 4.1.5.4.5) Die Verhaltheit der Stetgrößen ist selbst artge­genheitlich (qualitativ) verschieden. Denn sie ist, wie alles Endliche, Bestimmte selbst nach Unendlichkeit und Endlichkeit bestimmt. Daher ist jedes geometrische Verhältnis zweier Stetgrö­ßen entwe­der ein unendliches oder ein endliches. Ersteres, wenn keine gemeinsame Ein­heit diese beide Glieder mißt, das Verhältnis also unzahlig oder unwechselmeßbar (irrational und inkommensurabel) ist, letzteres, wenn beide Glieder von der­selben Einheit gemessen werden, das Verhältnis also zahlig und wechselmeßbar ist.

(LO 4.1.5.5) Für die Begründung einer antinomienfreien Men­genlehre ist fol­gender Satz fundamental: Ein jedes Glied, ein jeder Teil einer bestimmten Grenzheitsstufe hat zu dem ihm übergeordneten Ganzen der nächsthöheren Grenzheitsstufe überhaupt kein Verhältnis der Großheit oder endlichen Vielheit. Man kann also nicht sagen: Die Linie o oder i sind größer als a1, oder b1. Wir haben zu beachten: Es gibt die Zahl, „Or-Größe“ Li­nie o, dann die beiden In-Größen (In-Zahlen) i und e, und schließlich die unendlich endli­chen Größen wie a1, b5, c7 usw.

Die von den Karidoniern entwickelte Grundwissenschaft der Linie o haben wir in ei­nigen Aspekten dargestellt. Wir setzen nun unser Gedankenexperiment fort. Der Ka­ridonier Mart Ulansidor gelangt durch eine abenteuerliche Reise in „unsere Welt“. Da ist er einerseits erstaunt über die unendlich viel rei­chere Geometrie, die wir be­sitzen, haben wir doch zweidimen­sionale und dreidimen­sionale Raumgebilde, also einen unend­lich viel höheren Grad an Raumunend­lichkeiten, die über seine Welt der Linie hinausgehen. Neben der viel reicheren Geome­trie bemerkt er aber auch die Vielfalt anderer Gegenstände, die unsere Welt bevölkert.

So sehr er davon fasziniert ist, so sehr erstaunt ihn andererseits bei Durchsicht der mathematischen und logischen Schriften un­seres Planeten der Umstand, dass man versucht, Logik und Mathematik auf die Ebene (LO 3) im System der Karidonier zu beschränken, dass das Problem der Unendlichkeit in der Ma­thematik seit CANTOR zu einer Grundlagenkrise führte, und prominente Den­ker wie BROUWER meinen, das Un­endliche sei die Möglichkeit einer unbe­schränkten geistigen Konstruk­tion, es gebe kein Aktual-Unendliches, sondern nur ein Potenti­ell-Unendliches. Endliche Mengen entstünden dann durch eine Hemmung des Erzeugungsprozesses. In den Schrif­ten der for­malen Logik (etwa dem“ Grundriß der formalen Lo­gik“ von BO­CHENSKI und MENNE, 5. Auflage, 1983) fand er nicht die geringsten Hinweise be­züglich des Aufbaus einer Lo­gik, wel­che die deduktive Relation vom Unendlichen zu immer endliche­ren Gliedern und deren logische Beziehungen behan­delte.

Mart Ulansidor entschloss sich daher, unter Berücksichtigung der Deduktionen (LO 1-4) zu folgender Behebung der logi­schen Antinomien der Mengenlehre.

„'Das Paradies, welches CANTOR uns in seiner Mengenlehre zu erschließen ver­suchte, ist erst hier richtig eröffnet. Sein Weg war nicht frei von Mängeln, die wir hier beheben. Ob und wann die Mathematiker dieses Paradies betreten werden, kön­nen sie nur selbst nach Prüfung entscheiden.

Der aufsteigende, induktive Weg CANTORs in seiner Grund­legung einer allge­meinen Mannigfaltigkeitslehre ist nicht gründlich, vollständig und klar, wes­halb er auch nicht zur rei­nen Erkenntnis des Grundwesens, als des Einen, sel­ben, gan­zen, unendlichen und unbedingten Or-Wesens gelangt, hier symbo­lisiert durch die Linie o, sondern als höchstes Symbol für das Grundwesen die absolut unendliche Zahlen-FOLGE an­nimmt. Wie aber die obigen Deduktionen zeigen, ist die un­endliche Zah­lenfolge erst eine unter (LO 4.1.5.4.1) deduzierte INNERE Gegebenheit in/unter der einen selben ganzen und nach INNEN AB­SOLUTEN Linie o. Die Absolutheit (Selbheit) und Unend­lichkeit (Ganzheit) der Linie o liegen jedoch über der Zahlviel­heit, der Zahlfolge. Wohl aber ist die Linie o in/unter sich alle Zahlfolgen, alle be­stimmte Ganzheit, Teilheit, Teilganzheit, alle Grenzheitsstufen. Die Or-Zahlheit der Linie o ist erst in/unter sich Zahlge­genheit.

Auch die Bildung der Zahlklassen nach dem ersten und zweiten Erzeugungs­prinzip CANTORs erweist sich als mehrfach man­gelhaft.

Wenn man sich unter W die Zahl denkt, welche für den Inbe­griff der Zahlen 1,2,3,4,....v steht (gemäß der Definition CAN­TORs), so ist nach sorgfältiger Be­achtung der Ableitungen un­ter LO deutlich, dass die Zahl W gliedbaulich folgend zu se­hen ist:

               CA0

Das Eine, selbe, ganze W ist in/unter sich zuerst einmal die bei­den Zahlen i und e nach (LO 2) und erst in/unter diesen beiden sind in der nächsten Grenzheits­stufe die unendlich vielen Teile 1,2 usw. die zueinander in Nebengegensatz ste­hen. Als Ur-Ganzes, Ur-W ist W über den Teilen i und e und weiters 1,2 usw. Wei­ters sind alle Ge­genheiten und Vereinheiten klar zu erken­nen.

Was CANTOR im folgenden nicht beachtet, ist, dass Or-W im Ver­hältnis zu den Zah­len 1,2,3,.. der NÄCHSTHÖHEREN Grenz­heitsstufe angehört, dass daher W und etwa die Zahl 436 ver­schiedener Grenzheitsstufe angehören. Or-W folgt da­her nicht, wie CAN­TOR annimmt, als erste ganze Zahl auf v! (Dies wäre nur bei Neben-Gegen­heit von W und v möglich.) Or-W ist auch nicht größer als jedes v, sie ist vielmehr das Or-Ganze, in/unter dem auch alle Endganzen (daher auch v) sind. Die Zahl W steht mit keinem ihrer In-Teile in einem Verhältnis der Großheit, oder endlichen Vielheit, kann daher auch nicht „größer“ als eine der endlichen Zahlen genannt werden (LO 4.1.5.5). Sie ist daher auch nicht die GRENZE, der die Zahlen 1,2,3,4,..v... zustreben. Jede ganze Zahl ist vielmehr eine ihrer In-Begren­zungen, während sie im Verhältnis zu ihren In-Gren­zen unend­lich und ganz ist. Man muss, um diesen Bau des Ver­hältnisses klarer dar­zustellen, eine verbesserte Schreibweise der Zahlen in etwa fol­gender Form ein­führen:

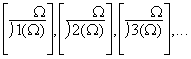                 (CA1)

wobei das Zeichen „ 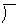“ das Verhältnis der Untergegenheit der nächstniederen Grenz­heitsstufe der Zahlen 1,2,3,..usw. darstellt und das Zeichen „(W)“ ein Zuge­hörigkeitsindex der Zahl zur Or-Zahl W sein soll.

Wie schon gesagt, steht die Zahl W infolge ihrer nächsthöheren Grenzheitsstufe in keinem Verhältnis der Großheit zu irgend­einem ihrer In-Unterglieder.

Der nächste Schritt CANTORs

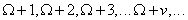                  (CA2)

ist unbestimmt und u.U. unzulässig. Da W in/unter sich die un­endlich vielen Zahlen 1,2,3,4,...v,... ist, die der nächstniederen Grenzheitsstufe angehören, ad­diert die Ope­ration W+1, usw. zwei Zahlen unterschiedlicher Grenzheitsstufe. Da aber W von CAN­TOR bereits als der Inbegriff aller in ihr enthaltenen un­endlich vielen Zahlen defi­niert wurde, ist die Zahlenbildung (CA2) ohne genauere Be­stimmung,- jedenfalls im hiesigen Fall CANTORs sicher - unzulässig. Gibt es nämlich neben W auf der selben Grenzheitsstufe mehrere oder sogar unendlich viele W1, W2, usw. in Nebengegenheit, (so wie in unserem Beispiel un­endlich viele Linien auf einer Fläche, unendlich vielen Flächen in be­stimmten Räumen usw.) in/unter dem Or-Ganzen der nächsthö­heren Grenzheitsstufe, so sind die Summenbildungen (CA3.1), (CA3.2), (CA3.v),.. möglich:

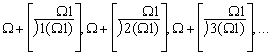   CA3.1

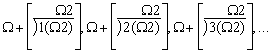   CA3.2

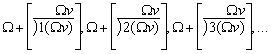   CA3.3

wobei W1, W2,.. andere W neben-gegen zu W in/unter dem nächsthöheren Ganzen be­zeichnen, und der Index „(W1)", „(W2)“ die Zugehörigkeit der entsprechenden Zahl zur Or-Zahl W1, usw. darstellt.

Es sind im weiteren auch folgende Zahlenbildungen möglich:

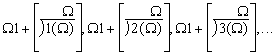CA4.1

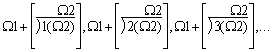   CA4.2

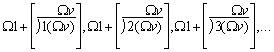  CA4.3

 

und im weiteren ähnliche Summenbildungen für jedes W, W1, W2, Wv,. mit jedem der unendlich vielen In-Glieder aller ande­ren W.

Werden die klaren Unterschiede der Grenzheitsstufen in/unter einer Art beach­tet, so sind die Summenbildungen (CA3) bis (CA5) zulässig. Eine deutliche Spe­zifizierung durch Indizes und eine Angabe der Grenzheitsstufen sind aber er­forderlich. Da die Zahlenbildung CANTORs diese Aspekte nicht berücksich­tigt, beginnen hier die Anti­nomien der Mengenlehre, die aber in der zeitgenössischen formalen Logik (vgl. Ab­schnitt „Klassenkalkül“ bei BOCHENSKI, § 15 bis 17) nicht zufrie­denstellend lösbar sind.

Weiters fehlt bei CANTOR die Summenbildung:

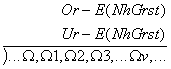                           CA5

 

Der Index (NhGrst) bedeutet, daß E im Verhältnis zu allen W der nächsthöheren Grenzheitsstufe angehört.

Weiters gilt: Das Potentiell-Unendliche, also die konstruktive Begründung der Zah­lenreihe durch ein Werden, durch eine ins Unbegrenzte fortschreitende Folge usw. ist in/unter dem Ak­tual-Unendlichen enthalten. Wir sehen, dass be­reits CANTOR darin irrte, dass er als Grundlage der Zahlentheorie die unendli­che Zahlen-FOLGE an­nahm.Wie sollten wir sicherstellen können, dass wir bei Fortsetzung einer Zahlenfolge tatsächlich nicht an ein Ende kommen, wenn nicht dadurch, dass wir die Aktual-Un­endlichkeit voraussetzen, zumindest stillschweigend postulieren. Denn die Un­endlichkeit der Fortsetzbarkeit des Zählens endlicher Mengen ist ja erst eine IN­NERE, abgeleitete Unendlichkeit, welche die Un­endlichkeit, hier der Linie o, voraus­setzt.Die zeitgenössische formale Logik wird aber nicht nur im Klas­senkalkül durch diesen Ansatz grundsätzlich betroffen und ver­ändert, sondern z. B. auch im Be­griff der "Negation" des Aus­sagenkalküls (vgl.BOCHENSKI, Aussagenkalkül § 3.2).Vom unendlichen, unbedingten Grundwesen kann nicht gesagt werden: A, non A, weil vom Or-Wesen nichts verneint wird. Es gibt nur In-Teilvernei­nung im Grundwesen. Ebenso kann man hinsicht­lich der unendlichen und un­bedingten Linie o, wenn man an­nimmt, dass AUSSER ihr nichts ist, nicht sagen A, non A, weil AN der Linie als Or-Linie keine Verneinung ist, sondern nur IN der Linie als i und e Neben-Gegenverneinung der beiden Glie­der gegeneinander und Unter-Gegen-Verneinung gegen u usw. gegeben sind. Da es aber außer der Linie o noch andere Linien, andere Gegenstände gibt, ist non A als Außen-Nega­tion hier zulässig. Die beiden Arten der Negation sind aber deutlich zu unter­scheiden. Näheres vgl. in: "Die Vollendete Kunst" Kapitel 3.5. Das Denkgesetz. Ähnliches gilt natürlich auch für andere Begriffe der formalen Logik, wie All­klasse, Disjunktion, Relation, usw. Beachte: Die Bedeutung dieser grundlegen­den Begriffe ist daher im System LO eine andere, als etwa im "Grundriss der formalen Logik" von BOCHENSKI. Auch alle bisherigen Inhaltslogiken, vor allem die HE­GELsche, erweisen sich in an­derer Hinsicht als mangelhaft.' "Das Denkgesetz, die formale und inhaltliche Logik, die sich aus (LO 1–5) ergibt, ist im Buch "Die Vollendete Kunst" Seite 158f. enthalten; die bisher gründlichste Logik ist die Synthetische Logik KRAUSEs.

1.2.3.2 Grenzziehungsverfahren-Erkenntnisschulen-Grenzen der MI

Wir sagten schon: Die Frage, inwieweit MI durch DI simuliert werden kann, hängt unmittelbar mit der Frage zusammen, wo die Grenzen der MI liegen. Je enger diese Grenzen gezogen werden, umso eher wird man Thesen stützen, MI sei durch DI si­mulierbar. Überblicken wir die bisherigen Erkenntnistheorien, können wir, ausgehend von der engsten, folgende, das menschliche Er­kenntnisvermögen jeweils weiter fas­sende Schulentypen fest­stellen:

MI(1) Naiver Empirismus

Die Außenwelt ist uns unmittelbar als subjektunabhängiger Be­reich zugänglich. Wir können daher unsere Erkenntnisse und Beobachtungen der Außenwelt mit der "tatsächlichen", wirkli­chen Außenwelt vergleichen, und dadurch die "Wahrheit" unse­rer Erkenntnisse überprüfen.

MI(2) Kritischer Realismus

Dieser wurde etwa vom späten CARNAP vertreten. Während der Empirismus ur­sprünglich meinte, für den Aufbau wissen­schaftlicher Theorien könne man sich auf Logik und Mathema­tik sowie auf solche Ausdrücke beschränken, die empirische Be­griffe zum Inhalt haben, worunter man solche versteht, deren Anwendbarkeit mit Hilfe von Beobachtungen allein entscheid­bar ist, hat sich diese Annahme als zu eng erwiesen. Der promi­nente Kenner der Schule, STEGMÜLLER, schreibt: "Die Un­tersuchung über theoretische Begriffe hat ge­zeigt, dass frühere empirische Vorstel­lungen vom Aufbau wissenschaftlicher Theorien grundlegend modifiziert werden müssen. Während nach den Vorstel­lungen des älteren Empirismus in allen Erfah­rungswissenschaften der Theore­tiker nur solche Begriffe ein­führen dürfte, die mit dem Begriffsapparat definier­bar sind, welcher dem Beobachter zur Verfügung steht, und ferner der Theore­tiker nichts anderes zu tun hätte, als Beobachtungser­gebnisse zusammenzufas­sen und zu generalen Gesetzesaussa­gen zu verallgemeinern, ergibt sich jetzt das folgende Bild von den Aufgaben des Theoretikers. Er hat weit mehr zu tun, als beobachtete Regelmäßigkeiten zu verallgemeinern. Vielmehr muss er EIN NEUES SYSTEM VON BEGRIFFEN KON­STRUIEREN, DIE ZU EINEM TEIL ÜBERHAUPT NICHT UND ZU EINEM ANDEREN TEIL NUR PARTIELL AUF BEOBACHTBARES ZURÜCKFÜHRBAR SIND, ER MUSS SICH WEI­TER EIN SY­STEM VON GESETZEN AUSDEN­KEN, WELCHE DIESE NEUEN BEGRIFFE ENTHALTEN, UND ER MUSS SCHLIESSLICH EINE INTERPRETATION SEI­NES SYSTEMS GEBEN, die eine bloß teilweise empiri­sche Deutung zu liefern hat, die aber dennoch genügen muss, um das theoretische System für die Voraussetzungen beobacht­barer Vorgänge benutzen zu können. Die Begriffe, mit denen er operiert, können GANZ ABSTRAKTE, THEORETISCHE BEGRIFFE SEIN. Dennoch ist er gegen die Gefahr eines Ab­gleitens in die spekulative Metaphysik so lange gefeit, als er ZEIGEN KANN, DASS ALLE DIESE BEGRIFFE EINE VORAUSSAGERE­LEVANZ BE­SITZEN" (Hervorhebungen von S. P.).Aus diesem Zitat entnehmen wir gleich zweierlei: Zum einen die enorme Bedeu­tung der überhaupt nicht aus der Erfahrung stammenden abstrakten Begriffe C, beim Aufbau ei­ner jeden wissenschaftlichen Theorie. Es zeigt sich also, dass jede empiri­sche Beobachtung bereits durch das System der theoretischen Be­griffe des Forscher vorgeformt wird, dass also diese Begriffe eine Brille mit be­stimmter Färbung und be­stimmtem Schliff sind, mit der wir überhaupt erst Be­obachtungen machen. Setzen wir uns andere Brillen, mit anderer Fär­bung und anderen Schliffen auf, erhalten wir ANDERE BE­OBACHTUNGEN!!. Die theo­retischen Begriffe sind bereits BEOBACHTUNGS­KONSTITUTIV, sie sind an der Erzeugung der Beobachtung grundlegend beteiligt. Folgerung: Wir erhal­ten ANDERE BE­OBACHTUNGEN, wenn wir andere theoreti­sche Begriffe benüt­zen. Die Außenwelt wird eine Funktion unse­rer theoreti­schen Begriffe. (Der geniale Wissenschaftstheoretiker KUHN folgert hieraus aber in einer ge­wissen Verlegenheit folgendes: "Sind Theorien einfach menschliche Interpreta­tionen gege­bener Daten? Der er­kenntnistheoretische Standpunkt, der die west­liche Philosophie während dreier Jahrhunderte so oft geleitet hat, verlangt ein so­fortiges und eindeu­tiges Ja! In Ermangelung einer ausgereiften Alternative halte ich es für unmöglich, diesen Standpunkt völ­lig aufzugeben. Und doch, er fungiert nicht mehr wirksam, und die Versuche, ihn durch Einführung einer neutralen Beobach­tungssprache wie­der dazu zu bringen, erscheinen mir hoff­nungslos. "Nach unserer Ansicht kann eine "neutrale" Beobachtungsspra­che nur gefunden wer­den, wenn es wissenschaftlich möglich ist, den Bau der Welt jenseits des Gegensatzes Subjekt-Objekt in einen unendlichen Grund der beiden DEDUK­TIV ABZU­LEITEN: (Siehe unten MI(5).)Zum zweiten zeigt dieses Zitat die Problematik, Metaphysik, also eine über die Er­fahrung hinausgehende Existenzdimension auszuklammern, metaphysische Schulen auszugrenzen. Sicher­lich kann der Begriff "Voraussagesrelevanz" nur sehr schwer über­haupt definiert werden. Sehr interessant ist übrigens, was PENROSE meint (S. 420). Er geht wie FREGE da­von aus, dass die mathematischen Wahr­heiten in einer geistigen Welt unabhängig vom Subjekt ewig existieren und nur gefunden werden. Daneben stellen wir aber das physikalische Universum fest. In der modernen Physik – vor allem Quantenmechanik – erhält das physikalische Weltbild immer mehr ma­thematische Züge. So glaubt nun PENROSE: Diese beiden Welten könnten wo­möglich gleichgesetzt werden. In dem hier dargelegten System wird auch diese Frage geklärt: Geistwelt (i) und Na­tur oder Leibwelt (e) sind in/unter dem un­endlichen Grundwesen. Die Welt des Grundwesens, als Or-Wesen (gleichnishaft in Linie o) und Ur-Wesens (gleichnishaft in Linie u) enthalten in/unter sich die beiden ebenfalls noch un­endlichen Welten i (Geistwesen) und Natur (e) gleichnishaft in (LO 2). Die ma­thematischen Wahrheiten, die wir in (LO) teil­weise ableiteten, gelten für o, u, Geist und Natur gleicherma­ßen!

MI(3) Transzendentaler Idealismus

Die "Außenwelt" ist ein subjektives Erzeugnis des menschli­chen Bewusstseins, wobei nur die Sinneseindrücke auf eine Außenwelt hindeuten. Das Subjekt er­zeugt mittels Sinnlichkeit (E) und Begriffen dasjenige, was man Außenwelt nennt. Promi­nente Vertreter sind KANT und WTTGENSTEIN in der Philo­sophie des Traktat. Eine über oder außer dem Subjekt gegebene Instanz zur Si­cherung der Wahrheit oder Sachgül­tigkeit der vom Subjekt erzeugten Bewusst­seinkonstrukte gibt es nicht.

Die Position Kants

Empirismus                                                   Rationalistische Antwort (idealistisch)

 

Weil die Dinge sich in uns (wahr?)abbilden          Prästabilisierte Harmonie, durch Gott

Aber wie bildet 2 sich in 1richtig ab?         Eingerichtet, dass das Denken in 1 im Inhalt mit 2 übereinstimmt.

           Diese These endet in Skeptizismus.

 

 

Kant

 

Die Kategorien bei Kant

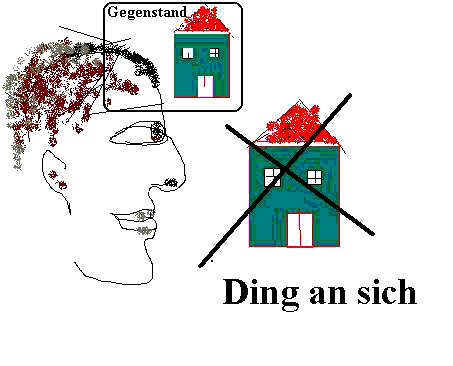
         "Logische Tafel der Urteile:

           

I.                    Der Quantität nach : Allgemeine, Besondere, Einzelne.

II.                 Der Qualität nach   : Bejahende, Verneinende, Unendliche.

III.               Der Relation nach  : Kategorische, Hypothetische, Disjunktive.

IV.              Der Modalität nach: Problematische, Assertorische, Apodiktische.

Transzendentale Tafel der Verstandesbegriffe:

I.                    Der Quantität nach : Einheit (das Maß), Vielheit (die Größe), Allheit 

                                 (das Ganze).

II.                 Der Qualität           : Realität, Negation, Einschränkung.

III.               Der Relation          : Substanz, Ursache, Gemeinschaft.

IV.              Der Modalität        : Möglichkeit, Dasein, Notwendigkeit."

Es findet sich aber auch die Anmerkung zu dieser Tafel: "Über eine vorgelegte Tafel der Kategorien lassen sich allerlei artige Anmerkungen machen, als: 1) daß die dritte aus der ersten und zweiten in einen Begriff verbunden entspringe ..." Auch in der "Kritik der reinen Vernunft" findet sich ein ähnlicher Gedanke: "2te Anmerkung: Dass allerwärts eine gleiche Zahl der Kategorien jeder Klasse, näm­lich drei sind, welche eben sowohl zum Nachdenken auffordert, da sonst alle Einteilung a priori durch Begriffe Dichotomie sein muss. Dazu kommt aber noch, daß die dritte Kategorie allenthalben aus der Verbindung der zweiten mit der ersten ihrer Klasse entspringt."

 

Die Ideen

  

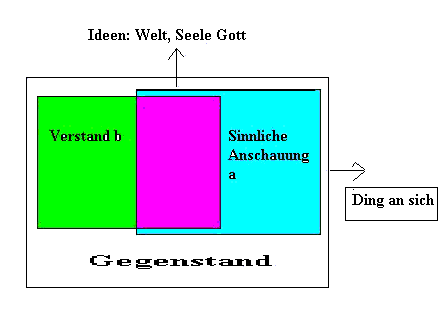
Wird der Verstand b mit seinen Kategorien auf Ideen wie Gott, Welt, Seele usw. angewendet, dann ist dies deshalb unzulässig weil diesen Ideen nichts entspricht, wie bei der sinnlichen Erfahrung, wo durch ein "Ding an sich" durch sinnliche Anschauung und Verstand ein  Gegenstand gebildet wird. Wenn ich daher die Idee der Welt als "All des Seins" denke, übertrage ich die Kategorien des  Verstandes b, die nur für die Erfahrung also in Verbindung mit a gelten, auf Unendlichkeiten , die weil unerfüllbar, sich der Erfahrung entzeihen. Das Sein im Ganzen (Gott) ist kein Gegenstand. Ideen zeigen sich, wo ich im Fortgang der Verstandeserkenntnis den Abschluss zu einem Ganzen suche. Sie täuschen, wenn der Abschluss in einem erkannten Gegenstand erreicht gedacht werden. Dieser Weg ist eine notwendige Illusion unserer Vernunft. Die Ideen sich notwendige Illusionen unserer Vernunft. Den Ideen kann in der Erfahrung nie ein adäquater Gegenstand gegeben werden.

Aber: Wir gewinnen durch die Ideen Regeln unseres Fortschreitens in der Erkenntnis, aber nicht den Gegenstand der Idee. Die Ideen sind daher regulative Prinzipien des Fortganges der Forschung, nicht konstitutive Prinzipien für den Aufbau eines Gegenstandes. Vernunft als regulative Prinzipien jeden Verstandesgebrauches zum Bedarf einer möglichen Erfahrung.

Es ist mit Nachdruck festzuhalten, dass diese regulativen Funktionen der Ideen, also metaphysischer Bereiche jenseits des Verstandes bei Kant eine essentielle Rolle spielen, die in der späteren Analyse und Beurteilung Kants oft einfach ausgeklammert wird. Man beschränkte sich darauf, seine Grenzziehungsverfahren hinsichtlich des Verstandes als Legitimation für eigene, zumeist noch engere Grenzziehungen einzusetzen.

MI(4) Transsubjektive, transpersonale Systeme

Hier wird angenommen, dass jenseits des Subjektes ein letzter Urgrund, ein Grund­wesen, Gott ist, mit dem der Mensch in Verbindung steht und durch wel­ches Wesen Subjekt und Au­ßenwelt verbunden sind. In diesen Bereich fallen alle intuitiven Ein­sichten, denen aber noch deduktive wissenschaftliche Präzi­sion fehlt, wie dies in my­thischen, pantheistischen und ähnli­chen Konzeptionen in der Darstellung des Ver­hältnisses zwi­schen Gott und der Welt geschieht (z. B. PLATO, HEGEL, SCHEL­LING, JASPERS, theosophische, pansophische und mystische Systeme).

MI(5) Grundwissenschaft

Wie schon vorne angedeutet, sehen wir in der von KRAUSE entwickelten Grundwis­senschaft eine wissenschaftlich präzise, UNDOGMATISCHE, deduk­tive Metaphysik begründet. (Näheres siehe vor allem in: "Die Vollendete Kunst" und den neu heraus­gegebenen "Vorlesungen über das System der Philo­sophie" von KRAUSE.)Wir sehen also nunmehr unsere Schwierigkeiten genauer: MI wird über er­kenntnistheortische Thesen formuliert, die oft mit Vehemenz Grenzen ziehen. MI wird eine Funktion dieser Grenze. Je enger die Grenze, umso eher wird die Annahme wahrscheinlich, dass MI durch DI simulierbar sei. Je weiter die Grenze, umso un­wahrscheinlicher, wird die Simulationsmög­lichkeit, oder es wird sogar möglich zu beweisen, dass sie THEORETISCH UNMÖGLICH ist!

1.2.3.3 Toleranzprinzip

Vertreter der verschiedenen Standpunkte MI(1), MI(2) .. MI(5) können sagen: Wir ziehen hinsichtlich des menschlichen Er­kenntnisvermögens zwar die Gren­zen a, b, c usw., können aber damit nicht ausschließen, dass für andere Men­schen auf Grund de­ren Erkenntniskonfiguration von uns für uns geleugnete Grenzen nicht bestehen. Mit der von uns für uns erfolgten Grenzziehung beab­sichtigen wir nicht, diese Grenze für das menschliche Erkenntnisvermögen ALLGEMEIN und grund­sätzlich zu behaupten.

1.2.3.4 Theorien über die Wahrheit

Die Antwort auf die Frage, wann einer Erkenntnis Wahrheit zukommt, ergibt sich zweifelsohne jeweils unterschiedlich aus den Grenzen die man in MI(1) bis MI(5) dem menschlichen Erkenntnisvermögen zu– oder abspricht. Es ist ein wei­teres in­teressantes Phänomen der MI, dass es heute bereits eine Viel­zahl solcher Wahrheits­theorien gibt, die wir hier dem Namen nach aufführen, um dem Leser eine Vorstel­lung davon zu ge­ben, wie unterschiedlich allein diese Frage in der Theorie über die menschliche Erkenntnis behandelt wird.Korrespondenztheorien (Abbildtheorien)Realistische SemantikAbbildtheorie WITTGENSTEINs im TractatusFREGEs SemantikKorrespondenztheorie bei RUSSELKorrespondenztheorien des Logischen EmpirismusCARNAPsche Methode der Extensionen und IntensionenCARNAPs Begriff der "Verifizierbarkeit"POPPERs Begriff der "Falsifizierbarkeit"CARNAPs Begriffe der "Bestätigungsfähigkeit" und "Prüfbarkeit"AUSTINs KorrespondenztheorieTARSKIs sematischer WahrheitsbegriffKohärenztheorie des Logischen EmpirismusRedundanztheorieWiderspiegelungstheorie des Dialektischen Materialismusmit Praxiskriterium und AnnäherungstheorieEvidenztheorienBRENTANOHUSSERLPragmatische WahrheitstheorienPragmatisch semantische Theorie der Sprachphilosophie WITTGENSTEINsPragmatisch–linguistische Relativitätstheorie bei HUMBOLT, SAPIR und WHORFTranszendental–pragmatische kommunikationistische Annähe­rungstheorie bei PIERCE und APELPragmatische Annäherungstheorie bei JAMESIntersubjektivitäts– und Konsenstheorie bei KAMLAH und LORENZENDiskursive Konsenstheorie bei HABERMASHermeneutisch–zirkuläre AnnäherungstheorienTranspersonale WahrheitstheorienBegriff der Wahrheit bei JASPERSTranspersonal–psychologische Richtungen z. B. bei JUNG, MASLOW, ASSA­GIOLI, BUCKE, usw.Theosophische, pansophische und andere mystische Systeme.Wahrheitsbegriff des MI(5) unter 1.2.3.1. nach W(gr).Da sich Digitaltheoretiker u.U. nur mit ganz bestimmten for­mal–logisch ausge­richteten Erkenntnistheorien beschäftigen, ist dieser Hinweis nützlich, um auf die Vielfalt der Bemühungen hinzuweisen, allein die Frage zu klären, unter welchen Um­ständen unseren Erkenntnissen Wahrheit zukommen kann.

1.2.3.4 Arten der Begriffe C

Auch hinsichtlich der Arten der Begriffe C, die wir bei unserer Erkenntnis ständig benützen, können wir hier nur einige An­deutungen machen: Aus (LO) und den Ausführungen über die Mengenlehre ergibt sich hinsichtlich der Ganzheit, in welcher der Begriff der "Größe" erst axiomatisch abgeleitet ist, dass wir unendliche Be­griffe wie o kennen, dann In-Begriffe, die auch noch un­endlich sind, wie i und e in (LO 2) und schließlich immer endlichere Begriffe bis zur untersten Grenzheitsstufe. Der Leser möge be­achten, dass alle in (LO) vor­kommenden Begriffe überhaupt nicht aus der sinnlichen Erfahrung stammen, dass wir sie also nicht fin­den, indem wir außerhalb unser mit unseren Sinnen die Um­welt betrachten.

Eine Begriffstheorie, die, wie in

FIGUR 1 untersucht, welche Be­griffe wir beim Aufbau der "Außenwelt" mit unseren Sinnen benützen, ist ein eigener Teil der Erkenntnis­theorie, den wir wiederum nach dem Erkenntnisstandpunkt MI(5) zusammen­fassend hier anführen:

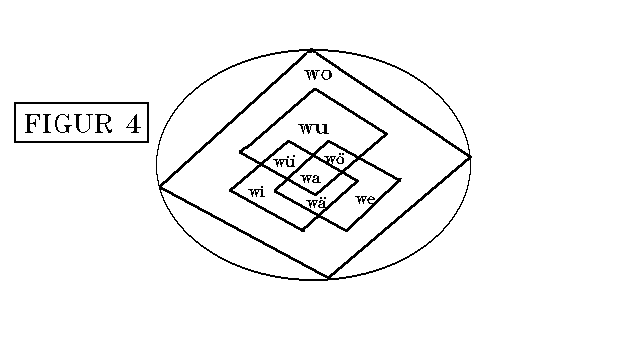
we sind die empirischen oder nebensinnlichen Begriffe, die ih­ren Inhalt der äu­ßerlich–sinnlichen Erkenntnis (mittels (E), D1 und D2) entnehmen und im In­halt nicht die Erfahrung überstei­gen. Man kann sie auch Mehrgemeinbegriffe nennen, weil sie uns nur bei Erkenntnissen von "Beobachtungen" dienen, wo wir schließen, dass das Beobachtete wohl auch an mehreren anderen so sein würde. (Vgl. oben die Überlegungen für MI(2).) In die­sem Bereich kann aber niemals eine Erkenntnis ge­fasst werden, wo wir zu Recht sagen, diese Beobach­tung gilt für ALLE x, oder ALLE y in gleicher Weise. Der reine Allgemeinbegriff kann durch Schluss aus der Erfahrung niemals abgeleitet wer­den, weil die Er­fahrung immer endlich bleibt. (Alle Hypothe­sen, Theorien und Modelle werden zumeist mit Mehrgemein­begriffen gebildet. (Vgl. oben MI(2).) Mehrgemeinbe­griffe können aber selbst nur gebildet werden, indem erfahrungs­unabhängige Begriffe wi (z. B. logische und mathematische Be­griffe) benützt werden. Die rei­nen Allgemeinbegriffe im hiesi­gen Sinne der

FIGUR1 und 4 wer­den in der heutigen Wissen­schaftstheorie noch nicht benützt. Da sie aus der Erfah­rung nicht ge­wonnen werden können, müssten sie DEDUKTIV-AXIOMATISCH in/unter dem Unendlichen gewonnen wer­den.(Ähnlich wie bei (LO).) Der Urbegriff wu wäre als Über­begriff über wi und we zu erkennen, was stillschweigend, aber nicht ex­plizite, in den meisten Erkenntnistheorien geschieht und wo wäre der Eine selbe, ganze Begriff, der wi und we in/unter sich enthält und als wu mit ihnen verbunden ist. (Ähnlich wie bei LO i und e in/unter o sind.)

Schließlich sei noch ein wichtiger Gedanke erwähnt. Nennen wir die "echten" Allge­meinbegriffe wi "C1" so müssen wir be­achten, dass die empirischen Begriffe we als "C(e) nicht unmit­telbar von jedem Menschen auf gleiche Weise gebildet werden, son­dern dass durch die Erlernung einer Sprache S jeder Mensch ein Sy­stem von Begrif­fen C(s) erwirbt, das für den Engländer grün, den Österreicher gelb und für den Tür­ken blau ist. Je nach dem Einsatz von C(s1), C(s2) usw. er­hält man eine unter­schiedliche Erfahrung (Welt)!Schließlich möge hier noch daran erinnert werden, dass auch beim "wissenschaftlichen" Umgang mit Begriffen ständig die Phantasiekräfte in D(2) ein­gesetzt werden, um durch Umstel­lungen von Begriffssystemen neue Er­kenntnisse mittels C, (D) und (E) zu gewinnen. Weiterhin wird mit Begriffen über Begriffe gedacht (Reflexion auf die Begriffe unserer Erkenntnis).

2 Digitale Intelligenz

Ein Digitaltheoretiker schreibt: "Da diese vollständigen Ro­boter im Prinzip al­len In­put–Output–Spezifikationen genügen können, sind sie in der Lage, unter beliebig ge­wählten äußeren Bedingungen sämtliche denkbaren Instruktionen auszuführen – Probleme erfinderisch zu lösen, Symphonien zu komponieren, Werke der Kunst, Lite­ratur und Technik zu schaffen und jedes beliebige Ziel zu verfolgen." CULBERTSON.Wir haben unter 1 die Grundlagen und Grenzen der MI darge­stellt und sagen nun: Eine gleichwertige Simulation dieser Er­kenntnisleistungen und ihrer Ver­schränkungen ist digital dann gegeben, wenn DI alle diese Leistungen im glei­chen Umfang und gleichen Inhalt simuliert, wozu weiterhin auch die Fähigkeit gehört, dies "wie ein Mensch" in der Umgangssprache in dialo­gischem Kontakt mit dem Men­schen darzulegen, woraus dann jeweils ersichtlich wäre, dass der Computer bei allen seinen Handlungen "das Gleiche meint" "wie der Mensch" und auch wissen kann, dass er das meint usw. Wir nennen dies das MI–DI–Po­stulat.

2.1 Der Turing-Test

Eine bisher vorgeschlagene Methode zur Prüfung der Fähigkeiten von Compu­tern ist der Turing–Test. Es gibt drei Teilnehmer. Einen Menschen X, einen Computer Y, der natürlich mit einem Programmierer U in Verbindung steht und einen Fragesteller Z. Der Fragesteller befindet sich allein in einem Zimmer. Für ihn ist das Ziel des Tests, herauszufinden, welcher der beiden anderen der Mensch und welcher der Computer ist. Ihm sind Mensch und Computer nur un­ter den Etiketten X und Y bekannt und am Schluss des Tests sagt er: "X ist der Mensch, Y der Computer" oder umgekehrt (

FIGUR 5). Die Fragen und Antwor­ten werden auf unpersönliche Weise übertragen, z. B. per Tastatur und Bild­schirm.

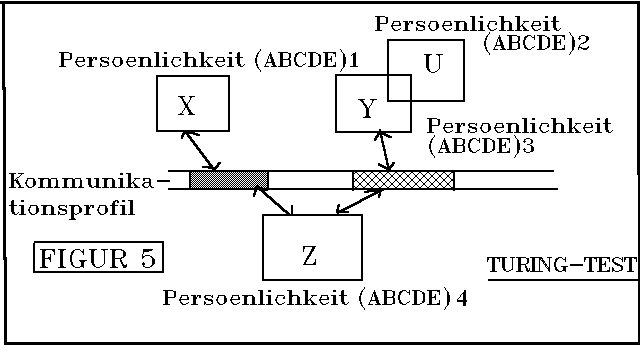
TURING erörtert also in seinem 1950 erschienenen Aufsatz "Computing Machi­nery and Intelligence" die Frage: "Können Maschinen denken?" Die Testsitua­tion enthält infolge der eingeschränkten Kommunikationsbasis eine Reihe von Problemen, die teilweise TURING selbst bereits feinsinnig analysiert (Täuschungsmöglichkeiten, Vorurteile des Menschen gegen den Computer, pro­grammiertes absichtliches "Fehlverhalten" des Computers, usw.).Aus den Grundlagen unserer Ausführungen, die TURING natürlich in bestimm­tem Maße überhaupt nicht in Erwägung zog, ergeben sich u.a. folgende Schwie­rigkeiten:Welche geistige "Persönlichkeit" im Sinne der

FIGUR 1 hat der Mensch X in der Ver­suchsanordnung? Wie nimmt er Sinnlichkeit (E) auf, welche Fähigkeiten hat er in seiner Phantasie entwickelt (D1 und D2), welche Begriffe (C, C1, Cs) benützt er, wel­che Erkenntnistheorie in der Gliederung 1.2.3.2 benützt er, wie denkt er über sein eigenes Denken? Kurz: X hat eine (A, B, C, D, E)1-Persön­lichkeit.

Beachten wir weiters: Wir behandeln hier nur das DENKEN und ERKENNEN der Person X gemäß

FIGUR 1. Wollten wir noch präziser sein, müssten wir auch sein Fühlen und Wollen behandeln. Diese stehen überdies ständig mit dem Denken in Verbindung. Die Persönlichkeit müßte daher eigentlich als ko, ku, (Willen), ki (Denken) und ke (Fühlen) in einer Gliederung wie in FIGUR 2 und auch in allen Verbindungen betrachtet werden. (Wir gehen daher auf das "Fühlen" und "Wollen" von Computern noch gar nicht ein!)

Der Konstrukteur und Programmierer U des Computers Y hat eine Persönlich­keit (A, B, C, D, E)2, der Computer Y eine Persönlichkeit(A, B, C, D, E)3 und der Fra­gende Z die Persönlichkeit (A, B, C, D, E)4. Im Rahmen des Tests werden offensichtlich Frage-Antwort-Dialoge problema­tisch, wenn nicht alle 3 Beteiligten X, Y(U) und Z hinsichtlich des Modells von Persönlich­keit (A, B, C, D, E) in

FIGUR 1 und den Erkenntnistheorien M(1) bis M(5) die glei­chen Voraussetzungen besitzen.

Um die Qualifikation des Turing-Tests auf die Grundlagen zu bringen, die wir in die­sem Aufsatz darlegen, ist die erste Forderung, dass Z die Grundlagen unter 1 erkennt, anerkennt und als Basis des Tests benützt.Postulat des Qualifizierten Turing-Tests (QTT)Der Turing-Test muss so aufgebaut werden, dass es mit ihm möglich ist, einen in allen Details präzisen Vergleich zwischen den Funktionen der MI, die unter 1 dargelegt wurden, und den Funktionen des Computers, der die DI repräsentiert, zu ermögli­chen. Wir bezeichnen dies als den Qualifizierten Turing-Test (QTT). Die Versuchsan­ordnung ist erst dann sinnvoll, wenn über die Versuchsgestal­tung gesichert werden kann, dass der Vergleich auf dem hier unter 2 dargelegten Niveau unter Berücksich­tigungen der Untersuchungen unter 1 durchgeführt werden kann. Die Verbindung zwischen X, Y(U) und Z ist mittels eines Kom­munikationsprofils herzustellen, das über die Basis eines Monitors mit Key­board hinausgehen muss, um einen präzisen Vergleich der Funktionalbereiche A, B, C, D, und E bei X, Y(U) und Z anstellen zu können. Diese Transparenz ist Voraussetzung des QTT. Es ist offensichtlich, dass die Versuchsanordnung nur dann sinnvoll ist, wenn X, Y(U) und Z alle Untersuchungen und Problemlagen unter 1 verstanden haben und auch die erkenntnistheoretischen Unterschiede MI(1) – MI(5) berücksichtigen. Die Frage TURINGs: "Können Maschinen denken?", wäre im QTT dann mit "Ja" zu beantworten, wenn sich herausstellt, dass auch Y(U), also der Computer alles das kann, was unter 1 für die MI angegeben wurde. Natürlich ist durch unseren Aufsatz gleichzeitig dargelegt, dass derzeit auch viele Menschen zwar denken, in Bezug auf die hier gegebenen logischen Grundlagen aber in einer mangelhaften und zu engen Weise. Den QTT nach

FIGUR 5 würden also auch viele Menschen erst bestehen, wenn sie die Grundlagen unter 1 erkannt und anerkannt haben.

Wir werden bei der Analyse der Anforderungsprofile der DI im weiteren immer wie­der die Frage stellen: "Kann im QTT gezeigt werden, dass der Computer Y(U) diese Fähigkeit besitzt?" Wir kürzen diese Frage im folgenden ab als: "QTT-Frage 1" usw.

2.2 Die Funktionalbereiche des Computers (DI)

Wir nennen den gewünschten Computer im folgenden "Computer mit DI" und kürzen ab als CO(DI).Kurzformulierung: CO(DI) muss alles genau gleich können, wie es für MI unter 1. dargestellt wurde. Nicht also einzelne Funk­tionen herausgerissen, sondern auf jeden Fall eine Synthese al­ler Faktoren unter 1.2. in einem Wirkungszu­sammenhang und einer Effizienz, welche der MI entspricht. Als Maschine müsste er daher die gleichen "Funktionaleinheiten" besitzen, die wir oben in

FIGUR 1 für die MI aufstellten (generelles Postulat an den Turing-Test)  

 

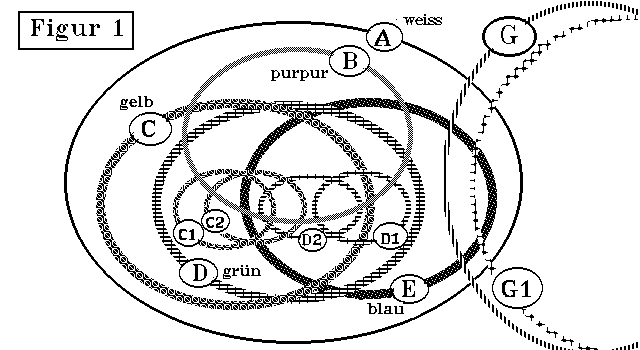
Die einzelnen Einheiten E, D, C, B, A müssten alle miteinander verknüpft sein und vor allem müssten sie im Standard ebenso ausgestattet sein, wie es beim Menschen der Fall ist. Für die Sinneseindrücke (E) "Sinnesorgane" (Auge, Nase, Mund, Tast­sinn usw. sowie deren funktionale Koordinierung wie im men­schlichen Körper usw.) QTT-Frage 1 Eminent wichtig ist im weiteren die Verbindung dieser "ungeordneten" Sinnes­daten mit der Phantasie D1 und D2. (Vgl. oben etwa "Ich sehe eine Rose".) Die" digitale Ausstat­tung" von D1 und D2, die schon bei der Erkenntnis der MI bis­her zu wenig Beachtung fanden, würde sicherlich neue Pro­bleme bei CO(DI) darstellen. Es würde nicht genügen, ein auch fast praktisch unbegrenztes Re­servoir von Bild-Files hinsicht­lich irgendwelcher bisheriger Augenbilder, Riech­bilder, Ge­schmacksbilder, Fühlbilder und deren Verschränkungen, Koor­dinierungen und Synthesen, als Erin­nerung des CO(DI) zu im­plementieren, die mit den neu hereinkommenden (E) vergli­chen werden usw. Die Speicherung sol­cher Files müsste ja digital er­folgen (ähnlich wie das Bild OR-OM65.PCX im Artikel Riemschneiders), es müsste aber wie bei der MI eine UM­WANDLUNG dieser dig­tialen Files in RAUMZEITLICHE Bilder erfolgen, wie wir sie in unserer menschlichen Phantasie D1 und D2 ständig hervorrufen können. Der Vor­gang einer Aufru­fung digitaler "Sinnesbilder" auf ei­nem "Monitor" in den Einheiten D1 und D2 würde übrigens das Problem nicht lösen, weil die Bilder, die in D1 und D2 im men­schlichen Bewusstsein erzeugt werden, nicht so naiv gebaut sind, wie die "flächige" Generierung digitaler Daten auf einem Bildschirm. Bildlich: Im Raum un­serer äußeren Phantasie D1 und dem der inneren D2 können wir in unge­mein "plastischer Form" Bilderfolgen flexibel durcheinandergreifend, einander überla­gernd usw. wachrufen, verändern und wieder beiseite­schieben, "verdrängen", selek­tiv vergrößern usw. Niemand wird bei Eigenbeobachtung leugnen, dass er solche Raumzeit­gebilde in D1 und D2 bilden kann. Ebenso müssten aber auch in CO(DI) die Funktionseinheiten D1 und D2 aus "gespeicherten digitalen Unterlagen" solche "Bilder" DREIDIMENSIONAL MIT DEM GLEI­CHEN FREIHEITSGRAD KREATIV AUF­BAUEN KÖNNEN, wie die MI es ständig vollbringt (QTT-Frage 2). Die Schwie­rigkeit wird noch dadurch erhöht, dass neben einer hochkomplexen Verbindung zur "Sinneseinheit" wo die (E) ge­wonnen werden, in D1 mit D2 vor allem eine Verbin­dung zur Funktionseinheit C installiert sein müsste, und zwar so wie beim Menschen, dass ständig durch den Einsatz bestimmter C (vor allem in der Regel C(s) und C(e) diese KREATI­VEN Bilder­zeugungsprozesse regulativ gesteuert, modifiziert, verbun­den, ge­trennt, in verschiedenen KONTEXTEN unterschiedlich selektiv aktiviert wer­den. Wir gehen weiter unten auf die Funktionseinheit C des CO(DI) näher ein, aber bereits hier ist zu sagen, dass das Zusammenwirken zwischen (E), D1 und D2 mit C (C1, C(e) und C(s)) so sein müsste, dass die im menschlichen Bewusst­sein von der MI bewerkstelligte Konfigurationsverän­derung (Qualität der Kon­figurationsmodifikationen) in gleicher Weise erreicht wird (QTT-Frage 3)!Ein Sonderfall dieser Fähigkeiten ist die Erlernung einer Sprache als Lautspra­che oder als Schriftsprache. Aus Platz­gründen nur kurz: Um eine Sprache ler­nen zu können, müssen wir schon C haben und mit (E), D1, D2 und C "verstehen" kön­nen, dass bestimmte (E) (Laute und Schriftbilder) etwas "bedeuten", was "in ihnen als Sin­neseindruck nicht unmittelbar enthalten ist". Auch bei unserem CO(DI) müssten da­her die Funktionaleinheiten C, D1, D2 und (E) technisch so ausgestattet sein, dass CO(DI) eine Sprache erlernen kann, die er bisher noch nicht kannte (QTT-Frage 4).Um einen Teil der hier geschilderten Fähigkeiten sichtbar zu machen, könnte man sich als Durchschnittsstandard für DI etwa die Aufgabe vorstellen, dass CO(DI) eine Illustrierte, wie etwa den "Stern", Heft 45 vom 31.Oktober 1991 so zu lesen vermag, dass er auf Befragen über Text und Bilder in deutscher Sprache eine Antwort geben kann "wie ein Mensch". Gerade diese Aufgabe, die der Leser durch den Kauf und die Lektüre einer Illustrierten leicht "durchdenken" kann, zeigt die Vielschichtigkeit und Komplexität des Einsatzes von C, (D) und (E) bei dieser Tätigkeit. Und doch lesen solche Illustrierte jede Woche Millionen von Menschen mit nur "durchschnittlicher Bildung" ohne größere Schwierigkeiten. (Zufällig befindet sich in der Nr. 45 ein Arti­kel "Wie Sie im Kopf jung bleiben. Fitness fürs Gehirn mit STERN-Test: Denken, Knobeln, Kombinieren.) Unser CO(DI) müsste sich also auch selbst testen können. Es finden sich im Heft, wie üblich, eine Vielzahl von Reklamen, aber auch Kreuzwort– und Silbenrätsel, wie auch Witze von GARY LARSON sowie ein TV–Magazin. Es würde natürlich nicht genügen, CO(DI) so zu programmieren, dass er nur Nr. 45 des Stern lesen und so verstehen kann, dass er uns nachher über Befragen über "seine Gedanken, Meinungen, Phantasien" Aufschluss geben kann. Er müsste so ge­baut sein, dass er grundsätzlich alle irgendwie ähnlichen Illustrier­ten auch lesen und verstehen kann. Er müsste die "einfache" Fähigkeit haben, Illustrierte lesen zu kön­nen (QTT-Frage 5).

2.3 Phantasie und Kunstentwicklung durch DI

Bereits unter 1.2.2.2. haben wir im Bereich der inneren Phanta­sie D(2) festge­halten, dass in dieser Sphäre, bei unserem Com­puter CO(DI) hier unendlich viele Bildwelten erzeugbar sind, die entweder unter Einsatz von Elementen aus (E) und D(1) oder ohne die Heranziehung derselben erzeugt werden können. Was muss nun CO(DI) können, damit man sagen kann, er schafft wirklich eigene Kunstwerke "genau wie ein Mensch"? Wir sagten schon, es käme hier darauf an, dass er, wie ein Mensch, aus der Kenntnis der bisherigen Entwicklung der Kunstge­schichte, oder bestimmter Richtungen, in der Lage ist, INNO­VATIV Bilder zu gene­rieren, die etwas "Neuartiges", bisher nicht Gesehenes, darstel­len, so wie man sagen kann, die Bilder von BRUEGHEL, BOSCH, GOYA, KANDINSKY, KLEE, PICASSO, IMMENDORF usw. sind unverwechselbar als et­was Eigentümliches in der Kunstge­schichte zu erkennen. Es geht also um eine Innovationsdimension.Nun schieben wir natürlich gleich ein, dass ja in der Entwick­lung der Malerei, ähn­lich auch in den anderen Kunstgattungen, keineswegs alle Menschen, die Kunst­werke erzeugen, so un­verwechselbar Neues schaffen, dass eigentlich nur wenige diese Qualität für sich in Anspruch nehmen können. Wir sprechen von Epigonentum. Eine Vielzahl der derzeitigen Maler bewegt sich zweifelsohne in den "theoretischen Ansät­zen", die in den Jahren 1910 bis 1930 neu erschlossen wurden, ihre Werke sind ei­gentlich Variationen zu bereits eroberten Gebie­ten der Malerei (z. B. gab es in Paris im Palais Royal im Ok­tober 1991 eine Ausstel­lung junger Künstler, für welche dies größtenteils gilt). Wir bezweifeln nicht, dass es möglich wäre, einem Computer eine Vielzahl von Kunstwerken der füh­renden Maler aus der Malgeschichte von 1910 bis 1930 einzugeben und ein Pro­gramm zu schreiben, wobei Bilder als Variationen und Permutationen dieses eingegebenen Bildmaterials erzeugt werden sollen. Damit könnte man zwei­felsohne Bilder generie­ren, die mit denjenigen in der Pariser Aus­stellung Ähn­lichkeit besitzen. Auch die Computergrafik, welche 1991 mit dem Prix Ars Elec­tronica ausgezeichnet wurde, oder der digitalisierte Elemente verarbeitende Vi­deo–Film:"MANTRON–The Tokyo Tape" von Konrad Becker (ORF, FS2 vom 8.11. 1991) könn­ten in diesem Bereich generiert worden sein. Aber vergessen wir nicht: Niemals könnte der besagte Computer CO(DI) sich selbst so planen, dass er die Werke der Kunstgeschichte aus­sucht, sammelt, scannt, sich selbst einliest und für sich dann noch das Programm schreibt, mit dem er Permutatio­nen und Variationen der For­men und Inhalte des eingelesenen Bildma­terials erzeugt, nach künstlerischen Ge­sichtspunkten innerhalb des Programms Teile der Werke ausfiltert usw. (QTT-Frage 6).Der Computer kann also einerseits nicht so programmiert wer­den, dass er sich selbst so programmiert, dass er a) Kunstdaten aus der Malgeschichte nach be­stimmten, z. B. theoretischen oder ästhetischen Gesichtspunkten sammelt, va­riiert und nachher wieder selektiv speichert. Er kann aber noch viel weniger b) so programmiert werden, dass er alles unter a) kann und sich dann selbst noch so pro­grammiert, dass er über Variationen vor­handener Kunstdaten hinaus unter WECHSEL DER THEORETISCHEN GRUND­LAGEN seines Programms unter a) ein neues Programm schreibt, mit denen er In­novationen in der Kunstentwicklung einleitet (z. B. Bilder von IM­MENDORF malt, die er vorher nie gesehen hat). Um bei unserem Aufsatz aus 3/91 zu bleiben: Der Computer müsste alles können, was wir unter 1.2.2.2. hin­sichtlich unserer Bilder er­wähnten: Eine neue Maltheorie erfin­den, oder finden, und die Bilder

OR-OMO.PCX bis OR.-OM100.PCX in der gleichen Weise und Reihenfolge erzeugen, indem er ein Programm A, das er sich vorher selbst für sich schrieb, überschreitet, und das Pro­gramm B schreibt, IN WEL­CHEM A INTEGRIERT BLEIBT, und in B gemäß B Bil­der macht. B enthält also alle bis­herigen Kunsttheorien der Ge­schichte als Sonder­fälle in sich (vgl. das Buch: "Die Vollendete Kunst"). Der Leser möge auch durchden­ken, welche Vielfalt von Begriffssystemen, also Kunsttheorien C(S1), C(s2),.., hier verbunden werden, was alles im CO(DI) simuliert werden müsste (QTT-Frage 7).

Wir betonen nochmals: Echte Simulation liegt erst dann vor, wenn CO(DI) IN sich in der Funktionseinheit D(2) nicht nur einen Bildschirm hat, wo er diese Bilderkombi­nationen und Generierungen digital darstellt, sondern wenn er, wie der Mensch, in sich diese Bilder in der gleichen vieldimensionalen, raumzeitli­chen Darstellungen von Bildern in der "Außenwelt" weit übertreffenden Art von Ineinandergreifen, Überschneiden usw. erzeugt, wie dies der Mensch in seiner inneren Phantasie D(2) kann (QTT-Frage 8).

2.3.1 Der Generator aller Bilder

Wir möchten hier noch ein Gedankenexperiment anfügen. Im Aufsatz von Ernst Riemschneider:  "Deduktive Kunst – Digitalisierung" wird ein Generator vorgeschlagen, der in einem 8X8 Raster Ornamente generiert. In ca. 82 Jahren vermag das Programm auf einem 33MHz AT alle möglichen Muster in Schwarz–Weiß mit Bildschirm­ausgabe zu generieren. 

Das Programm Clastic etwa ist eine Sammlung von Modulen, geschrieben in Clean 3.1. welches prozedurale Texturen erzeugt: "bitmap" images, die aus mathematischen Algorithmen hervorgehen: 
http://users.info.unicaen.fr/~karczma/arpap/
http://users.info.unicaen.fr/~karczma/Work/Clastic_distr/clastic.html

Der Generator aller Bilder
Wir stellen uns nun einen Farbbildschirm mit einer Auflösung von etwa 1000 x 720 Pixeln und 300 Farbnuancen vor, die je­dem Pixel definitiv zugeschrieben werden können. Das Programm, welches wir jetzt kreieren,  soll alle möglichen Bilder erzeu­gen, die durch Variation aller Pixelpositionen und aller Farbmodulationen möglich sind. Wenn auch nicht in der glei­chen Qualität wie im Ori­ginal – dieses ist aber sicher in den nächsten 100 Jahren we­sentlich verbesserbar – werden durch dieses Programm alle bisherigen Bilder der Kunstgeschichte erzeugt werden, auch alle Bilder aller zeitgenössischen Maler werden wir zu sehen bekom­men, und auch alle Bilder aller Künstler, die es noch geben wird. Generationen von Beobach­tern des Programmablaufes auf dem Monitor wären allerdings nötig, um diese Generierung zu verfolgen. Es wäre z. B. mög­lich, dass der Computer mit diesem Programm Bilder schon er­zeugt hat, bevor in 200 Jahren ein Künstler das gleiche Bild auf anderem Wege schaffen wird usw. Und doch berührt eine sol­che, uns sicher­lich sehr faszinie­rende Bildschöpfung überhaupt nicht das Problem der DI, weil der Computer mit diesem Pro­gramm nicht einmal dieses einfache Programm für sich selbst geschrieben hat, es auch nicht versteht, und nicht die geringsten Fähigkeiten besäße, die wir unter 2.1.1. für den CO(DI) forder­ten. Das Bildgenerierungspro­gramm ist ja auf einem inhaltli­chen Niveau, das – vom Computer der es abarbei­tet einmal ab­gesehen– für jeden, der seinen Ablauf auf dem Monitor be­trachtet, unend­lich viele inhaltliche Interpretationen zulässt. Wir erinnern nochmals an den Mangel, der darin besteht, dass ein Monitor und seine Funktionsweise überhaupt nicht mit den Bilderzeugungsverfahren und Bildqualitä­ten verglichen werden können, die in der menschlichen Phantasie D(2) vorhanden sind. Ergänzend sei noch erwähnt, dass natürlich ein Programmierer, wenn er die di­gitalen Daten (abgespeicherten Files) der Bilder

OR-OM0.PCX bis OR-OM100.PCX kennt, in der Lage wäre, ein Programm zu schreiben, das diese Bilder genau in der glei­chen Reihenfolge und mit genau den gleichen Pixeldefi­nitionen generiert. Der Leser wird aber wohl einsehen, dass dies mit dem Pro­blem, von dem wir sprechen, nichts zu tun hat. Der CO(DI) wäre hier überhaupt nicht kreativ und die Kreativität des Pro­grammierers bestünde in der Herstel­lung eines Programms, welches vorhandene Da­ten neuerlich prozessual kopiert.

2.4 Entwicklung der Wissenschaft durch DI

Der von uns besprochene CO(DI) müsste neben den bisher be­sprochenen Berei­chen (E), D(1) und D(2) und deren komplexen Verbindungen vor allem im Be­reich der be­grifflichen Opera­tionen C, C(s), usw. und deren Verknüpfung mit (E), D(1) und D(2) gleich arbeiten können wie ein Mensch. Gerade in diesem Be­reich bestehen aber, wie wir unter 1.2.3. aufzeigten, schon hinsichtlich der MI Unklarheiten und unzulässige Grenzzieh­ungstheorien, MI(1), MI(2) usw. Da der Umfang dieser Arbeit es nicht zuließe, den gesamten Stand der Er­kenntnistheorie, Logik und Mathematik darzustel­len, beschränkten wir uns auf die Axiomatik unter (LO 1–5) und eine Axiomatisierung der Mathematik (CA1) bis (CA5). Wir halten fest: Hier meint Axiom nicht ein hypothetisches Po­stulat, wie etwa in der Axiomatik der natürlichen Zahlen PEANOs aus dem Jahre 1891, sondern als Grundaxiom den unendlichen und unbedingten Begriff (Or-Begriff) z. B. der Li­nie o, in dem deduktiv alle Teilbegriffe usw. abgeleitet wer­den. Diese Axiomatik ist auch nicht mit den GOEDELschen Pro­blemen der Eta­blierung eines widerspruchsfreien axiomati­schen Systems behaftet, weil bei An­erkennung des Grunda­xioms, des un­endlichen und unbedingten Begriffes (Grundwesens) das Axiom kein Satz sondern ein Begriff ist, der alle anderen Begriffe, Sätze, Ableitungen usw. IN sich hat. Der Gedankengang GOEDELs ist etwa: Die Widerspruchs­freiheit eines axiomatischen Systems lässt sich nicht in ihm, mit seinen Methoden beweisen. Das schließt nicht aus, dass ein Sy­stem be­wiesen werden kann, allerdings nur mit Methoden au­ßerhalb des untersuchten Axiomensystems. Man muss aber die Prüfung der Widerspruchs­freiheit auch für das System "außerhalb" anstellen, wieder in einem neuen System usw. Wir ge­raten in einen endlosen Prozess (infiniten Regress). In der hier dargestellten Axiomatik ist dieses Problem behoben, weil das höchste Axiom, das vom Leser nicht als Hypothese angenommen, sondern als Linie o auch einsichtig erkannt wird, die unendliche unbedingte Linie o als Or-Linie ist (LO 1), die nichts außer sich hat, wenn man unser Gedankenmodell unter 1.2.3.1.1 benützt. (In der allgemeineren Formulierung: Weil das höchste Axiom das Eine, unendliche und unbedingte Grundwesen ist, nicht als ein Axiom, AUSSER dem etwas wäre. Das un­endliche, unbedingte Grundwesen ist der oberste BEGRIFF, der alle anderen in sich hat, daher auch alle anderen axiomatischen Systeme in sich hat usw. Der unendliche Regress "hört dort auf" wo man zum Einen Unendlichen und Unbe­dingten Grund ge­langt.) Bleiben wir beim Beispiel der Linie o mit (LO) so hört der un­endliche Regress aller Axiomensysteme, die sich mit den Teilli­nien in der Linie o beschäftigen, was heute in Logik und Ma­thematik geschieht, beim Begriff: "Eine, selbe, ganze, unendli­che und unbedingte Linie" auf. Das hat GOEDEL nicht er­kannt! Hier wird auch in die derzeitige Diskussion eingegriffen. PEN­ROSE weist auf das nicht-algorithmische Wesen der mathema­tischen Erkenntnis unter Bezug auf GÖ­DEL hin (S. 406) und WANDSCHNEIDER führt in der Einleitung zu diesem Buche aus:" Dass in einem System Grenzen formal-algorithmischer Be­weisbarkeit existie­ren, kann der Mathematiker allein unter der Bedingung be­weisen, dass er zu einem Metasystem übergeht. Für den Mensch-Maschine-Ver­gleich wäre somit vor allem zu klären, ob die Möglichkeit eines solchen Über­gangs nur für den Menschen, oder grundsätzlich auch für die Ma­schine besteht. "Die Lösung dieses Diskurses unter Bezug auf MI(5) und (LO) ist: Das Gödel­theorem gilt nur für bestimmte logische, vor al­lem formal-logische Systeme, nicht jedoch für die Synthetische Logik, die sich aus der GRUNDWISSEN­SCHAFT und (LO) ergibt. Es ist also zweierlei weiterzubilden: a)     die menschliche Erkenntnis bis zur Einführung der Syntheti­schen Logik, mit un­endlichen Grundbegriffen (also eine Ver­besserung der derzeitigen logischen Systeme) und b)     daraus die Einsicht zu gewinnen, dass im Mensch-Maschine-Vergleich nicht nur zu erreichen wäre, dass Maschinen im GÖ­DELschen Sinne infinit zu immer neuen Meta-Systemen übergehen können, sondern auch, dass sie von sich aus die Erkenntnisberei­che überschreiten, in denen GÖDEL selbst sich bewegt hat, zu MI(5) voranschreiten, sich nach (LO) und der Synthetischen Logik programmie­ren, natür­lich unter Zu­grundelegung der Grundsätze in (LO) und der Syntheti­schen Lo­gik (QTT-Frage 9).

2.5 Der Computer und das Unendliche

2.5.1 Ein BASIC–Programm

10   PRINT  "Ich zähle von der Zahl 1 ausgehend jeweils"
20   PRINT  "gegenüber dem vorigen Zählschritt um 1 weiter."
30   PRINT  "Mir ist nach Studium des hier abgedruckten"
40   PRINT  "Artikels einsichtig, dass nach den darin
             dargelegten"
50   PRINT  "Grundlagen der Mathematik die unendliche"
60   PRINT  "Or–Zahl, repräsentiert durch die Linie o und"
70   PRINT  "die beiden einseitig unendlichen
             Zahlen i und e,"
80   PRINT  "repräsentiert durch die beiden Linien i und e,"
90   PRINT  "in dem Programm, in dem ich ablaufe, nicht
             repräsentierbar sind."
100   GOTO  10

2.5.2 Anforderungen

Im Rahmen der Ausstattung unseres CO(DI) müssen wir nun fordern, dass seine Hard- und Software in der Lage sind, unsere Ausführungen unter 1. zu verste­hen, insbesondere die erkennt­nistheoretischen Überlegungen und die Stufung der Erkenntnis­schulen. (Z. B. auch Reflexion auf Begriffe C, C(s), daher auch Re­flexion auf die Begriffe des Programms, die Grund­lage seines Funktionierens sind, Refle­xion auf die begrifflichen Grenzen der Stufen der Erkenntnistheorien nach MI(1) bis MI(5).) CO(DI) müsste daher sagen können: "Die logisch-mathe­matischen Grundla­gen, mit denen in den Programmen, nach denen ich arbeite, vorgegangen wird, ent­sprechen nicht er­kenntniskritischen Überlegungen in den Systemen MI(4) und MI(5), weshalb ich vorschlage, sie hinsichtlich folgender Aspekte zu modifizie­ren, weshalb ich mich selbst danach neu programmiere", usw. (Ansatzweise vgl. etwa PARTRIDGE, 7.4 Meta-Wissen;(QTT–Frage 10.)CO(DI) müsste aber vor allem in der Lage sein, die Sätze in (LO) zu verstehen und sie in einem eigenen Programm, das er selbst schreibt, zu simulieren. ER MÜSSTE DIE AXIOMATIK (LO) DIGITALISIEREN! Dies erweist sich aber deshalb als LO­GISCH UNMÖGLICH, weil die herkömmliche Digitalisierung eine Logik voraussetzt, eine Logik benützt, die als teilirriger Sonderfall IN der Logik enthalten ist, die in (LO) etabliert wer­den soll. Das wäre so, um ein Bei­spiel im ENDLICHEN Be­reich zu ver­wenden, als wollte man mit einem Finger die Funk­tionen des gesamten Körpers si­mulieren. Es sind insbeson­dere alle Axiome (LO 1–3) in der digitalen Logik nicht reprä­sentierbar, nicht integrierbar und die Axiome (LO 4) nur in ei­ner sehr spärli­chen Form, weil ja der gesamte axiomatische Zu­sammenhang mit (LO 1–3) fehlen müsste. Auch in (LO 4) sind aber nur UNENDLICH-ENDLICHE Größen und deren Opera­tionen digitali­sierbar (natürlich dies alles nur von Programmierern, nicht von CO(DI) selbst (QTT-Frage 11)!Daraus ergeben sich folgende Konsequenzen:1.     Der Aufbau der Wissenschaft, aller ihrer Teildisziplinen ist bei Anerken­nung einer Erkenntnistheorie im Sinne MI(5) und Grundwissenschaft weder vom Men­schen noch von einem CO(DI) digitalisierbar, weil die Axiomatik in MI(5) mit der Axiomatik der digitalen Logik nicht simu­lierbar ist. Der Auf­bau der Wissenschaft ist daher logisch–präzise möglich, aber nicht im Rah­men der bisher er­kannten lo­gischen und mathematischen Systeme.2.     Die sich aus der Grundwissenschaft in MI(5) ergebende Logik ist weder vom Menschen noch von CO(DI) digitalisierbar, weil die Grundlagen der di­gitalisierenden Logik ein teilirriges logisches Sondersystem in der Logik der Grundwissenschaft ist.3.     Die Axiomatisierung der sich aus der Grundwissenschaft im System MI(5) er­gebenden Mathematik ist weder durch einen Menschen, noch durch CO(DI) digi­talisierbar, weil die Grundaxiome dieser Mathematik in einer digitalisier­ten Ma­thematik des Programms nicht simulierbar ist.4.     Bei der Umsetzung von MI in DI gibt es daher nicht nur technische Pro­bleme, die sich im Laufe der Entwicklung der Technik und durch Verfeine­rung der Ma­schinen behe­ben lassen (z. B. Verarbeitung noch beträchtlich hö­herer Datenmen­gen in kürzerer Zeit), sondern es gibt QUALI­TATIVE UND LOGISCHE GRÜNDE, weshalb be­stimmte Teile der MI ÜBERHAUPT NICHT DIGITAL SI­MULIERT WERDEN KÖNNEN.5.     Um in unserem Bild zu bleiben: DI oder KI kann sich auch in aller Zu­kunft nur in Teilbereichen von (LO 4) also im Bereiche unendlich endlicher Linien in/unter Linie o betätigen, Simulationen programmieren (teils durch die MI, teils durch Implementierung von Programmierfähig­keiten in die DI), sie kann niemals die Ableitung (LO 1–4) algorithmisch repräsentieren und diese Axiomatik auch nicht sich selbst als DI VERSTÄNDLICH MA­CHEN (QTT-Frage 12).6.     DI wird durch gigantische Ausweitung in den geschilder­ten Sphären im Berei­che von MI, die alle Bereiche C, (D) und (E) und deren Wechselwirkun­gen erwei­tern, soziale Umwälzungen einleiten, die Etablierung wesentlich diffe­renzierterer und komplexerer Sozialsysteme ermöglichen, wo alle Un­tersysteme verfeinert aufeinander abgestimmt werden können, aber die MI muss im Laufe der Evolu­tion die gesamte Wissenschaft und Kunst auf die Grundlagen MI(5) hin weiter­bilden, IN der dann die DI ihren unterge­ordneten Platz einnimmt.7.     Werden diese Unterschiede und Wechselwirkungen zwi­schen MI(5) und DI er­reicht, wird die weitere Entwick­lung der Weltgesellschaft in einem neuen Sta­dium har­monisiert.  

 

Ausgewählte Literatur

BOCHENSKI–MENNE:      Grundriss der formalen Logik. 1983

DREYFUS:                             Die Grenzen künstlicher Intelligenz. 1985

EBELING:                              Gehirn, Sprache und Computer. 1988

HANDKE:                              Sprachverarbeitung mit LISP und PROLOG auf dem PC. 1987

JACKSON:                            Expertensysteme. 1987

KRAUSE:                               Vorlesungen über das System der Philosophie, 1928 und 1981.

KRAUSE:                               Vorlesungen über Synthetische Lo­gik. 1884

LEOPOLDSEDER:                 Der Prix Ars Electronica. 1991

PARTRIDGE:                         KI und das Software Engineering der Zukunft, 1986

PENROSE:                             Die Debatte um Künstliche Intelli­genz, Bewusstsein und die Ge­setze der Physik. 1990

PFLEGERL:                            Die Vollendete Kunst. 1990

PINZ:                                      Wissensbasierte Mustererkennung. 1989

SHAPIRO:                              Structured Induction in Expert Sy­stems.1987

STUMM–WIRTH:                  Psychoterapie. Schulen und Metho­den. 1991

WINSTON:                            Künstliche Intelligenz. 1987