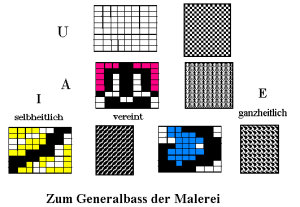Deduktive Kunst

Deduktive Kunst – Digitalisierung

Ernst Riemschneider

Dass  die elektronischen Medien die in der Schriftkultur ent­wickelten
Gesell­schaften, die sich vor allem seit der Erfin­dung der
Buchdruckerkunst bildeten, völlig verän­dern wer­den, ist durch die
wichtigen Untersuchungen Marschall Mc LUHANs [1]
gesi­chert. Auch in der Kunst haben die neuen Medien zu
wir­ken begonnen. Wenn auch der internationale Kunstmarkt Pro­dukte der
Ölmalerei, die den traditionellen Me­dien zugehören, mit Preisen umwälzt,
die bisher nicht er­reicht wurden (z.B. van GOGH), ist dies doch kein
Anzei­chen für eine Zu­nahme an gesamtgesellschaft­licher
Bedeu­tung.

Die Kunsttheorie für digital erzeugte und dargestellte Raum(zeit)gebilde aller Art
steckt in den Kinderschuhen. Die we­nigen Künstler, die bisher mit diesen
Medien umgehen, sind häufig unbelastet von der gesamten bisherigen
Kunsttradi­tion, viele ihrer Werke muten daher, wenn man sie in den
Gesamt­konnex der bisherigen Kunstäußerungen der Menschheitsge­schichte
einordnet, an, als wollte uns ein Rad­fahrer einreden, er führe mit einem
Porsche. Jede revolu­tionäre Neuerungsbe­wegung neigt auch dazu, das
Bisherige vorerst krass und di­stanzierend abzulehnen.

Die
folgenden Zeilen sind eine Anregung, ein Entwurf von Grundlagen einer Kunst­theorie für digital erzeugte und re­produzierte Raum(zeit)gebilde. Sie basiert auf einer Kunst­theorie, die alle bisherigen in sich enthält, die aber über diese auch
weit, ja auch über alle möglichen Kunstäußerungen der digitalen Kunst,
hinaus­reicht. Wenn wir hier Anregungen für die Kunstheorie der Digitalkunst
geben, so ge­schieht dies gleichsam „zurück aus der Zukunft“. [2]

1 Allgemeines

  Eine ausreichend profunde Kunsttheorie für digital erzeugte und dargestellte
Kunstwerke muss zumindest in großen Zügen alle bisherigen Kunstäußerungen
ken­nen und – auch wenn sie darüber hinausgeht – berücksichtigen. Nur so ent­geht sie ei­ner derzeitig verbreiteten Naivität. Ihr ist es aber auch infolge ih­rer technischen Fä­higkeiten gegeben und sie ist dazu berufen, eine Integration und Verbindung aller bisherigen Kunstäuße­rungen herzustellen. Damit leistet sie einen wichti­gen Schritt für die weitere Entwicklung der Kunst überhaupt.
Ei­nige An­sätze hiezu seien im fol­genden gegeben.

2       Der Raum

Die Raumtheorie
Peter WEIBELs

  Ein Pionier der elektronischen Kunst, Peter WEIBEL, sieht die Entwicklung in der bildenden Kunst durch die elektroni­schen Medien etwa darin, dass der
Grundsatz der Zentralper­spektive, die seit der Renaissance gültig war,
auf­gelöst wird. An die Stelle eines zentralen (feudalen) Uni-Versums,
treten gleich­zeitig nebeneinander beste­hende auf­einander bezogene, multi­ple Bilder und Modelle, in einem Pluri-Versum. Nicht zentral auf einen Punkt hin ausgerich­tete Teil-Räume beste­hen neben­einander, ineinander usw. „An die Stelle desUni­versums mit einem einzigen, gül­tigen Standpunkt tritt eine
pluriverse Welt vieler Standpunkte.„ [3]

„Die
neue Sprache des Raumes ist der Output einer Gram­matik, die eine
un­endliche Zahl von Modellen erzeugt, wo die räumli­chen und zeitlichen
Bezie­hungen veränder­bar sind.“

Die folgenden Seiten zeigen, dass diese Raum(zeit)theorie noch unvollständig
ist.

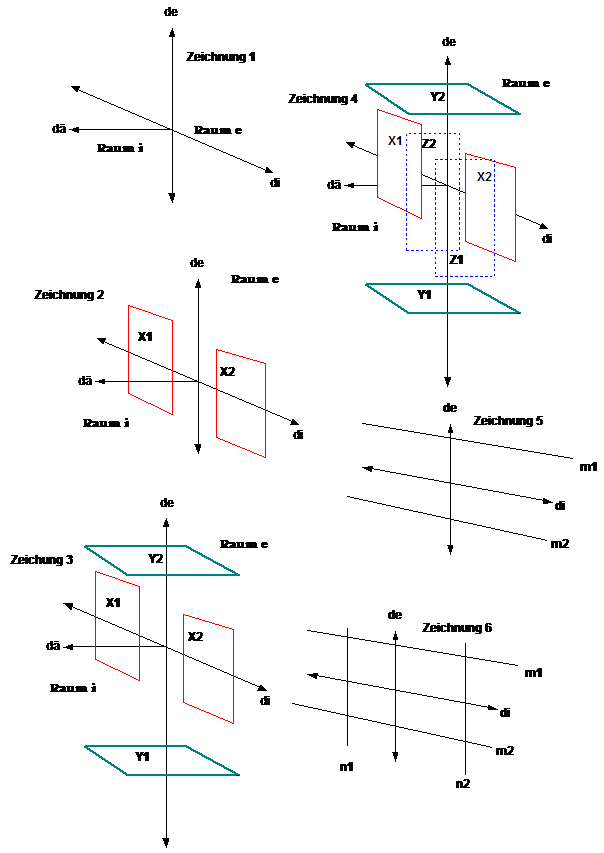
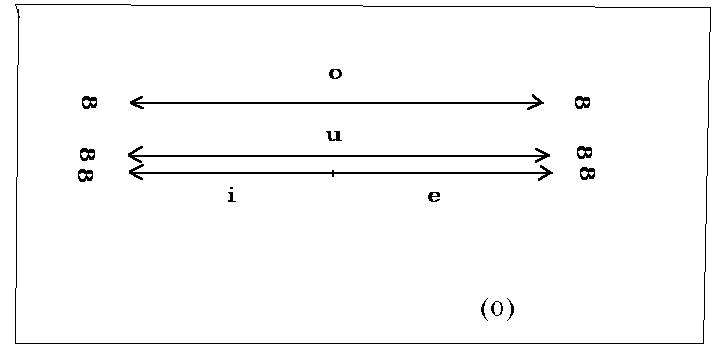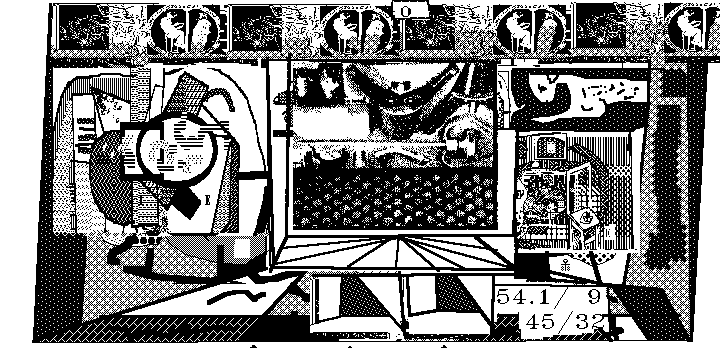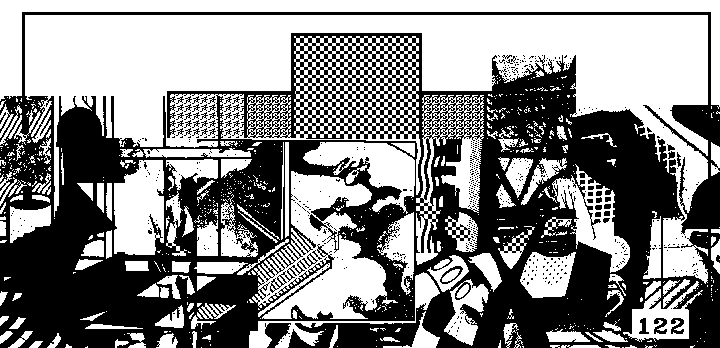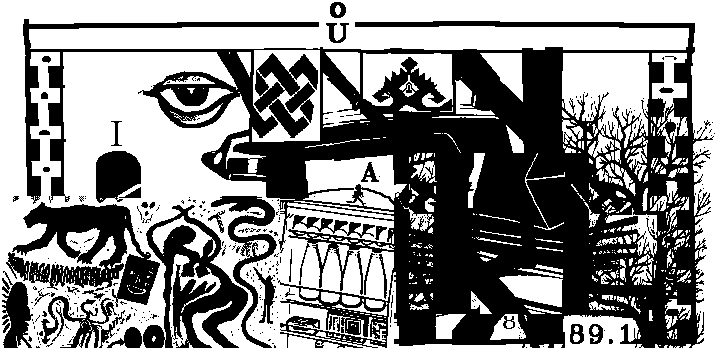
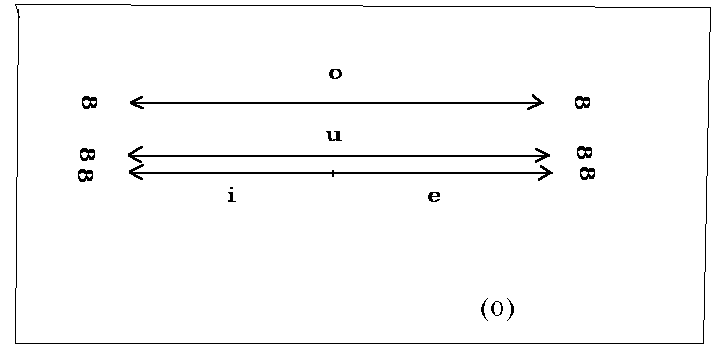
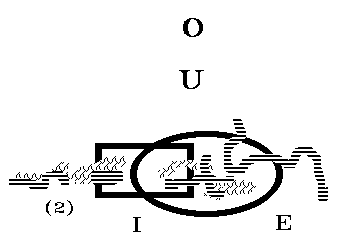
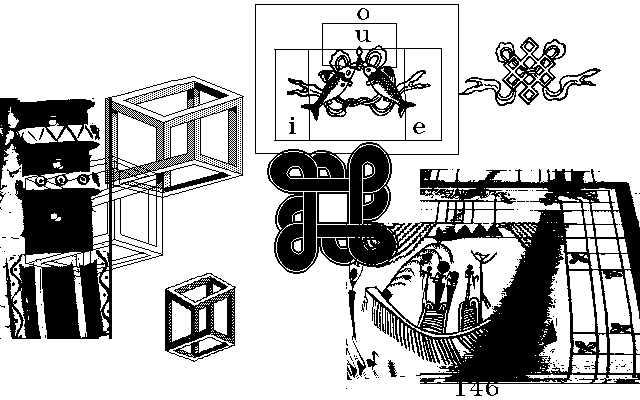
2.1. Räume

Der unendliche und unbedingte Raum o (Or-Raum) ist in
allen drei Richtungen unendlich, hat also keine Grenzheit hinsichtlich der
Richtheit. Der Räume i und e in Zeichnung 1, haben ebenfalls hinsichtlich keiner
Richtung eine Grenze, sind also auch in alle drei Richtungen unendlich. Wenn
auch die Richtung dä in zwei Hälften zerfällt, so ist doch das halbe dä in
Richtung i unendlich lange, wie auch in Richtung e. Die Räume i und e haben
daher die selbe Grenzheitstufe, wie der Raum o (Or-Raum).

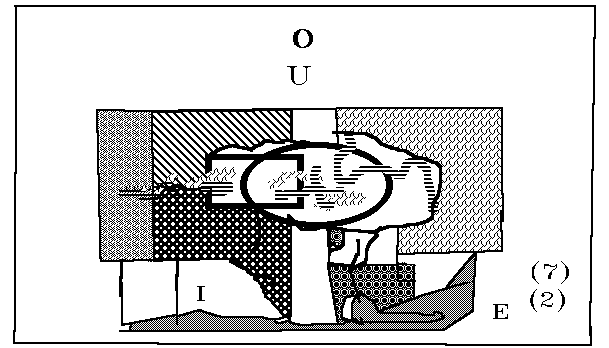
Die nächste Grenzheitstufe des Raumes in sich ist
durch zwei unendliche rote Flächen als Grenzen bestimmt, wie in Zeichnung 2
dargestellt. Der Raum zwischen den roten Fläche X1 und X2 ist daher nur mehr in
2 Richtungen unendlich, in einer Richtung aber endlich. Dieser Raum G ist
hinsichtlich der Grenzheitstufe von den Räumen i und e sowie dem Or-Raum o
artheitlich unterschieden. Zu beachten ist, dass ein solcher Raum sowohl in i
als auch in e als auch in beiden sein kann.

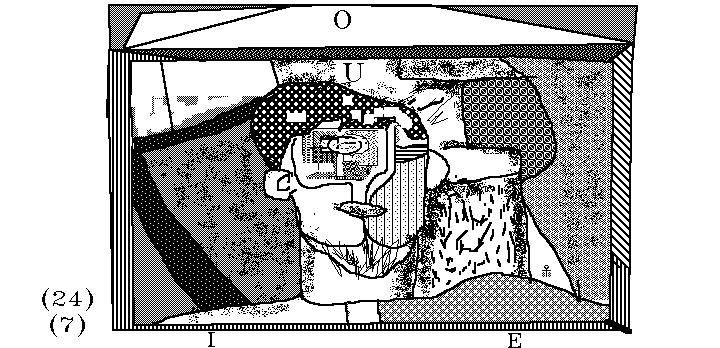
Die nächste innere Art der Grenzstufheit der Räume ist dadurch gegeben, dass in einer zweiten Richtung Endlichkeit gegeben ist. In Zeichnung 3 ist eine unendlich lange, viereckige Säule gegeben, die durch die unendlichen roten Flächen X1, X2 und die unendlichen grünen Flächen Y1, Y2 begrenzt ist. Auch hinsichtlich der Richtung de ist nun Grenzheit gegeben,
hinsichtlich di aber immer noch Unendlichkeit. Auch ein solcher Raum kann in i,
e oder in beiden gelegen sein.

Schließlich ist noch eine dritte Art der Grenzheitstufung des Raumes zu erkennen, wenn nämlich in allen drei Richtungen Endlichkeit gegeben ist, wie in Zeichnung 4, wo durch die Begrenzung der endlichen roten Flächen X1, X2, endlichen grünen Flächen Y1, Y2 und endlichen blauen Flächen Z1, Z2 ein Würfel oder Quader entsteht. Endlicher kann ein Raum
nicht mehr werden. Er ist unendlich endlich. Der Raum hat also in sich 3 Arten
von In-Räumen.

2.2. Flächen

Fläche gilt als Raum ohne Tiefe. (Nicht im Sinne nicht-euklidischer Geometrien, für welche natürlich modifizierte Regelungen gelten, hinsichtlich der Frage der inneren Grenzheitstufen aber die gleichen Kategorien modifiziert Anwendung finden müssen.) Im üblichen Sinne ist dahe Fläche definiert als Raum mit zwei Dimensionen. Auch hier gilt wieder, dass bei der ersten In-Gliederung der unendlichen Fläche in Zeichnung 1 durch die Linie di zwei Teile der Fläche entstehen, die jeweils den oberen Teil der Richtung de und den unteren Teil derselben befassen, dass aber in der Richtung de keine Grenzheitstufe der Fläche gegeben ist, weil de in beide Richtungen noch unendlich lange ist.

Erst wenn, wie in Zeichnung 5 durch zwei Linien m1 und
m2 die Richtung de endlich wird, z.B. 3 cm lang, entsteht eine Fläche mit der
ersten inneren Grenzheitstufe der Fläche, eine Fläche also, die in der Art von
der unendlichen Fläche und den beiden Hälften derselben unterschieden ist. Die
Fläche M ist nur mehr in einer Richtung unendlich. Die Fläche hat aber noch eine
weitere innere Grenzheitstufe, die in Zeichnung 6 dargestellt ist. Wird auch die
Richtung di endlich, durch die beiden Geraden n1 und n2, entsteht eine in jeder
Richtung endliche Fläche. Die Fläche hat also in sich zwei Arten von In-Flächen,
die nach der Stufung der Grenzheit unterschieden sind.

2.3. Linie

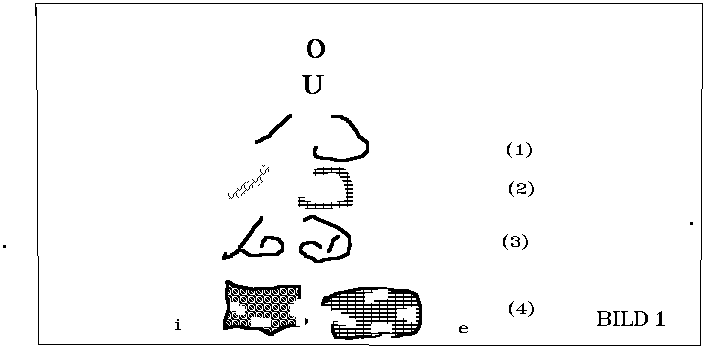
 Hinsichtlich der Linie und ihren Grenzheitsstufen sind folgende Deduktionen zu beachten:

Betrachten wir die Linie (1), so ist sie eine
unendlich lange, gerade Linie o.

Nun blicken wir auf die Linie (2), die schon in der Linie (1) ist. Sie zeigt uns, was die Linie (1) in sich ist. Die Linie (1) ist in sich zwei und nur zwei Linien, i und e,
die beide noch unendlich lang, aber doch insoweit gegenheitlich sind, als die
eine ist, was die andere nicht ist und umgekehrt, das heißt, sie verneinen und
begrenzen einander teilweise. Jede der beiden ist zwar noch unendlich lang, aber
der Punkt x ist ihre Grenze gegeneinander.

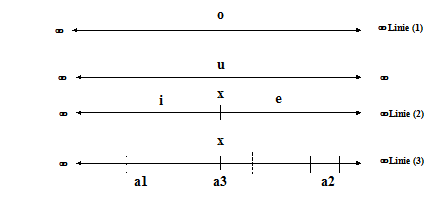
Hier in dieser ersten Ableitung der Linie (1) nach innen erkennen wir, dass es in der ersten Ableitung nach innen,
wenn man von einem unendlichen Ganzen ausgeht, nur zwei Glieder gibt, die beide
noch unendlich sind. Die beiden Linien haben daher die gleiche Grenzheitstufe,
wie die Linie o. Wir sehen weiter, dass hier eine Neben-Gegen-Verneinung von i
und e entsteht, wodurch aber die Linie (1) in keiner Weise negiert wird. Was
heißt der Begriff Neben-Gegen-Verneinung? Die Linie i ist neben der Linie e,
aber die eine ist, was die andere nicht ist und umgekehrt.
Betrachten wir jetzt die Linie (1) mit der Linie (2) in Verbindung, so
wird sichtbar, dass die Linie (1) als Ur-Linie über i und e steht und mit
beiden verbunden ist. Als Ur-Linie ist die Linie (1) über beiden, die beiden
sind unter ihr.

Die Linie (3) zeigt die zweite Stufe der Ableitung nach innen. Wir sehen, dass es in der Welt der Linie (1), in der zweiten Stufe nach innen, neue Arten von Linien gibt. Auf der Linie i gibt es unendlich viele Linien (a1, b1 usw.). Auf der Linie e gibt es unendlich viele Linien (a2, b2 usw.). Es gibt jedoch auch unendlich viele Linien, die sowohl auf i als auch auf e liegen (a3, b3 usw.). Diese beidseitig begrenzten Linien gehören daher einer neuen Art von Linien an, die bilden die letzte Grenzheitstufe der Linie nach innen. Begrenzter, als auf beiden Seiten begrenzt, kann eine Linie nicht sein.

2.4.   Ergebnis für die Raumtheorie

Alle Arten von beidseitig in di und de begrenzten Flächen sind enthalten in/unter der unendlichen Fläche, die nach dem Prinzip von 4 Stufen der Begrenzung nach innen begrenzt ist, wie oben abgeleitet. Peter WEIBELs Theorie des Raumes bewegt sich nur im Bereich endlicher Räume und Flächen (begrenzte Plutriversen), ohne dass die genaue Ableitung der Räume, Flächen und Linien erkannt wäre. Das Pluriversum aller begrenzter Flächen  ist in/unter der einen selben ganzen nach innen unendlichen Fläche enthalten oder die Ganzen Fläche ist in/unter  sich Ar­ten von Flächen gemäß den Ableitungen. Oder die eine unendliche Fläche ist in sich, in deutlichen Begrenzungsstufen die All-Heit der erwähnten Flä­hen. Das Endliche ist im Unendlichen enthalten, die Begrenzung des Endlichen nach innen erfolgt stufenweise.

2.5.   Das Elektronische Raumkonzept WEIBELs

Das
oben erwähnte Raumkonzept WEIBELs geht von folgender Evolution aus: Die
Auflösung des Raumbegriffes, welcher der Kunstgestaltung seit der Renaissance
innewohnt, ist im elektronischen Zeitalter gleichzeitig:

Zersplitterung
des einheitlichen Raumkonzeptes (Kubismus), Integration des Zeitbegriffes in den Raumbegriff (Futurismus) und in der elektronischen Kunst, Integration
unterschiedlicher Raumganzer, räumlicher Einheiten in neuen Synthesen (auch mit Zeit) gemäß dem 3. Abschnitt des II. Hauptlebensalters

WEIBEL
schreibt: „Die neue Sprache des Raumes ist der Output einer Grammatik, die eine
unendliche Zahl von Modellen erzeugt, wo die räumlichen und zeitlichen
Beziehungen veränderbar sind.(…) Im Spiel der räumlichen Codes, der spatialen
Signifikanten, wo Ein-Richtungs-Gegenstände zu Mehr-Richtungs-Gegenständen
werden ( z. B. Tisch eine Lampe) erhebt und entfaltet sich das Subjekt im
entgrenzten, ungemessenen Raum.“

Dieses Raumkonzept, welches erkenntnistheoretisch als ein subjektivistisches Raumkonzept bezeichnet werden kann, zeigt erkenntnistheoretisch den Übergang von einem naiven Empirismus zu einem kritischen Realismus oder gar transzendentalen Idealismus: „Nicht mehr die Objekte sollten den Raum definieren, sondern der Geist, der den Raum und die räumlichen Parameter wie Entfernung und Größe nach Belieben korrigieren und variieren kann.“ Oder: „HEINZ VON FOERSTER behauptet, dass wir die Wirklichkeit eher konstruieren bzw. erfinden, als dass wir sie entdecken oder finden.“

Auch der elektronische Raumbegriff WEIBELs bleibt aber:

a) subjektiver, Raumbegriff;

b) das „befreite“ Subjekt agiert in Partialräumen, Partial-Raum-Codes,
ohne im Sinne der erkenntnistheoretischen Entwicklung den Or-Om-Code
(All-Code) des Raumes und der Zeit zu erkennen.

c)Auf die geschilderte Weise sind unendlich viele Raumkonzeptionen,
Gegenstandsformationen möglich, die aber alle über das Unendliche am Endlichen, am Teilhaften, Begrenzten nicht hinausgelangen zum Unendlichen, Orheitlichen, in/unter dem sie dann erst die Endlichkeit im Unendlichen und vor allem die Unendlichkeit am Endlichen erkennen können. Diese Konzepte WEIBELs bleiben daher im 3 Abschnitt des II Hauptlebensalters stecken.

Man kann bildlich sagen, dass das Raumkonzept im Universum der geraden Linie nur die Linie (L3) erkennt, dass aber die Linie (L1) und darin die Linie (L2) nicht erkannt werden und damit auch die Deduktion von (L1) bis (L3) nicht erkannt werden.

Noch ein Wort zum Begriff des Pluriversums bei WEIBEL: Nach seiner Ansicht wird von dem (feudalen) Ein-Partialraum der Renaissance übergegangen zum Pluripartialräumen, aus der Einheitlichkeit in die Vielfalt der Partialräume. Nicht erkannt werden aber die weiteren Evolutionsstufen, nämlich dass alle diese möglichen Partialwelten, Pluriversen
in/unter dem unendlichen Wesen, Gott,
als in ihm gegliederte Partialwelten sind. Hier fehlen vor allem die Stufungen des Unendlichen ins Endliche.
Die Entwicklung wird daher fortschreiten: Von den Pluriversen, Partialversen
des 3. Abschnittes des II. Hauptlebensalters, welche die elektronischen Medien
bereits erzeugten, zu den Grunderkenntnissen des III. Hauptlebensalters der
Allsynthese, wonach alle endlichen, begrenzten Pluriversen in/unter Or-Wesen
erkannt werden sowie räumlich und zeitlich in/unter dem Or-Raum
und der Or-Zeit.

2.5.1. Ergebnis für die Raumtheorie

Alle Arten von beidseitig in de begrenzten Linien sind ent­halten in/unter der
beidsei­tig in de unendlichen Linie (1), die nach dem Prinzip von 2 Stufen
der Be­grenzung nach innen be­grenzt wird. Das Pluriversum aller
begrenzten Linien ist in/unter Linie (1) enthalten, oder Linie (1) ist in sich
Arten von Linien (i und e; a1, b1, usw.). Oder: Die Linie (19 ist in sich in
deutlichen Begrenzungsstufen die All-Heit der erwähnten Li­nien. Das
Endliche ist im Un­endlichen, logisch gestuft, enthalten.

2.5.2.  Endliche Linien werden weiter geteilt

In der aktuellen Fraktalgeometrie werden endliche Linien nach weiteren
ma­thematischen Regeln geteilt, wobei Compu­terprogramme in der Lage
sind, sol­che Li­nien darzu­stellen.“ [4]
Eine Linie kann in N identische Teile geteilt werden, von denen jeder
im Verhältnis r=l/N zum Gesamten steht. Bei ei­nem selbstähn­lichen
Objekt von N Teilen, die im Verhältnis r zum Ganzen skaliert wurden, ist seine
fraktale oder Ähnlich­keitsdimension mit D = log(N)/log(l/r) gegeben. Z. B. N=4, r=1/3, D= log(4)/log(3) = 1,26. In diesem Fall wird ein ein­faches Liniensegment gedrittelt und das mittlere Seg­ment wird ersetzt durch zwei gleiche Segmente, die Teil eines gleichseiti­gen Dreiecks sind. Auf der nächsten Stufe der Kon­struktion wird jedes die­ser vier Segmente durch vier neue Seg­mente mit
ei­ner Länge von 1/3 ihrer Herkunfts­segmente aus dem ur­sprünglichen Muster er­setzt. Dieser Vorgang, im­mer wieder wiederholt, ergibt die wunderschöne KOCHsche Kurve. (KOCHKURV.PCX)

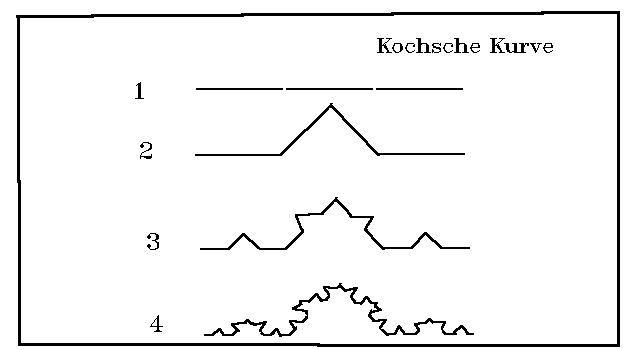
Das beweist, dass die Wiederholung einer sehr einfachen Re­gel scheinbar
kom­plexe Formen mit ganz außergewöhnli­chen Ei­genschaften ergeben
kann. Die Kurve besitzt eine ge­naue Selbstähnlichkeit. Jeder kleine Teil
ergibt durch Vergröße­rung ganz ex­akt einen größeren Teil. Auf jeder
Stufe ihrer Kon­struktion nimmt die Länge der Kurve mit einem Faktor von 4/3
zu. Eine unendlich lange Linie begrenzt daher eine end­lich große Fläche
auf der Ebene, ohne sich selbst zu durch­kreuzen. (Vgl. die Ableitungen
unter 2.2 und 2.3, die in der Fraktalgeometrie bisher nicht be­rücksichtigt
wurden. Die KOCHsche Kurve zeigt, dass eine endliche Li­nie im Sinne 2.3.3
weiter unendlich teilbar und bestimmbar ist.

3. Die Zeit

  Die Zeit ist die Form des stetigen Übergehens eines endli­chen Zustandes eines
Endli­chen in den nächsten. So kann beispielsweise eine Li­nie Ä von 3
cm dauernd kürzer, wieder länger und wieder kür­zer werden, sich stetig
ändern in ihrer Ausdeh­nung; oder eine Pflanze keimt, wächst, blüht und
verwelkt. Die Form die­ses Än­derns ist die Zeit. Die Zeit kann
vergli­chen werden mit der Linie Y unter 2.3. Die Zeit ist nicht endlich
son­dern un­endlich. Sie hat keinen Anfang und kein Ende. Sie ist durch
den Zeit­punkt f geteilt in die beiden un­endlichen Teile J (Vergangenheit) und E (Zukunft). Die Zeit ist also erst in sich Vergangenheit, Gegenwart und Zukunft. Die Zeit ist mit dem Raum insoweit vereint, als Endli­ches, Bestimmtes, Räumli­ches in sich die Form der Zeit hat, inso­fern es von einen be­stimmten Zustand in einen anderen übergeht (z. B. eine Fläche A3, die sich dreht, fortbewegt, größer oder kleiner wird; eine Katze die ge­zeugt, geboren wird, wächst und stirbt). Der
un­endliche, un­bedingte ganze Raum hat daher die Zeit nur in
sich, er ist aber selbst nicht in der Zeit.

4.  Theorie elementarer Formen

Die obigen Ausführungen über Raum und Zeit sind für eine allumfassende Theorie der Formen fundamental. Die Arten der Formen von Raum(zeit)gebilden
gliedern sich vom Un­endlichen zum Endlichen in der unter 2. geschilderten
Weise. Dies ist die Ur–Grammatik der Formen. Die Kunst kann nur ganz endliche Formen in einer den körperlichen Sinnen wahr­nehmbaren Form darstellen; sie kann hierbei je­doch u. U. mit endlichen Formen Unendliches auszudrücken
ver­suchen.

Die digitale Kunst erweitert die Möglichkeiten der Darstel­lung von
Raum(zeit)gebilden.

4.1    Ein Generator elementarer Formen

Einige Grafikprogramme besitzen eine pixelorientierte Funk­tion zur Erzeugung von schwarz-weißen (s/w) oder fär­bigen patterns (Mustern, Ornamenten). Die Er­forschung der bishe­rigen Muster, Ornamente und patterns in der Kunstge­schichte erscheint nicht sehr systematisch und gründ­lich. [5]

Wir können nur schwer die Frage klären, was sich die Künst­ler dachten, die vor
5.000 Jahren auf die Wand einer Kult­stätte ein Muster zeichneten. Neben
so­ziologischen, histo­risch-künstleri­schen Untersuchungen ist auch daran zu erin­nern, dass in den Symbolen der Geheimlehren (z.B. I Ging, Kabbala) elementare geometri­sche Formen eine Rolle spiel­ten. Wie weit sind solche Hintergründe in der Geschichte des Ornamentes wirksam (sakral-esoterische
Ornamentik)?

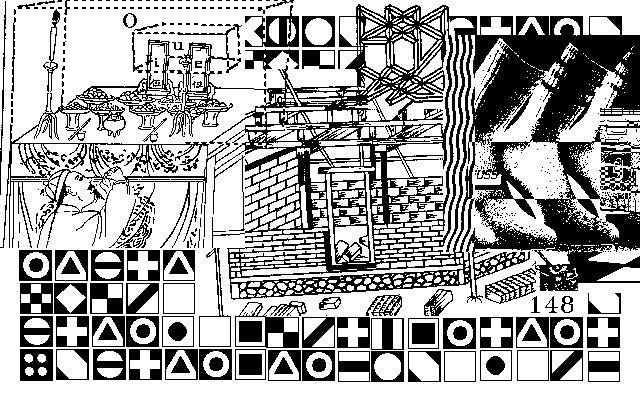
Im Grafikprogramm Paintbrush z.B. gibt es eine „Edit
pat­tern“-Funktion, bei der eine Fläche in 8 x 8 Quadrate geteilt ist. Jedes
der 64 Felder kann im S/W-Mo­dus schwarz oder weiß sein. Es gibt daher 2⁶⁴ Möglichkeiten die Felder mit s/w zu bele­gen, also 2⁶⁴ verschiedene Ornamente.

(Nehmen wir an, dass die 32 Schachfiguren 32 verschiedenen Farben
entspre­chen, die bei der Mustererzeugung benutzt wer­den. Wenn wir
nunmehr nur jene Posi­tionen berücksichtigen, die nach den Schachregeln
sinnvoll sind, erhalten wir alle mögli­chen Posi­tionen, die logisch im
Schachspiel möglich sind).

In anderen Grafikprogrammen können 16×16 Quadrate be­setzt werden. Der
Reich­tum an Elementarformen nimmt zu.

4.1.1    Die magischen Quadrate

Magische Quadrate sind dadurch gekennzeichnet, dass in den Unterquadraten die Zahlen ab 1 bis zur Höhe des höchstelli­gen Quadrates so eingetragen wer­den, dass die Summen in den waagrechten und senkrechten Reihen, sowie in den
Diagona­len gleich sind. z.B.

 

Zeichnen wir hier jeweils die ungeraden Zahlen s ein, erhal­ten wir ein
regelmä­ßiges Muster. In unserem Grafikpro­gramm von 8×8 Pixeln können
wir alle ma­gischen Quadrate bis 8 x 8 dar­stellen und ihre reichhaltigen mathematischen Eigen­schaften untersuchen.

Ein Beispiel für das magische Quadrat 8 x 8:

 

Versuche hier die ungeraden Zahlen s zu zeichnen. Du er­hältst ein regelmäßiges
Mu­ster, eines in den 2⁶⁴, die wir oben be­sprochen haben. Es besteht daher auch ein ma­thematischer Zu­sammenhang zwischen Regelmäßigkeit und bestimmten Zah­lenverhältnissen, zwischen Schönheit und mathemati­schen Maßverhältnis­sen. Oder: Jedes der 2⁶⁴ Muster hat ganz be­stimmte mathematisch-ästhetische
Eigenschaften.

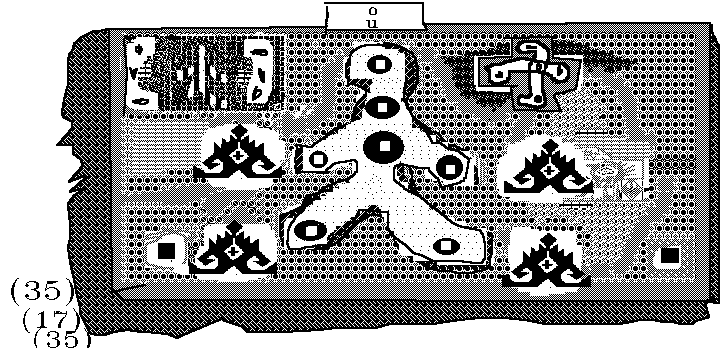
4.1.2  Einige Arten von 8×8-Ornamenten

Die beiden Muster all.1 und all.2 sind gegliedert wie der Raum, die Fläche (2.2)
oder die Linie (2.3) in sich, aber eben mit ganz endlichen Flächen. (ALL12.PCX)

eq.1
und eq.2 sind an der senkrechten Mittelachse gespiegelt. (EQ12.PCX)

Invsv. 1
sind invertiert/seitenverkehrt. (INSV1.PCX)
Die un­terste Zeile ist die inver­tierte der obersten und so nach innen.

Reg.1
ist um die Mittelachse regelmäßig. (REGIRREG.PCX)

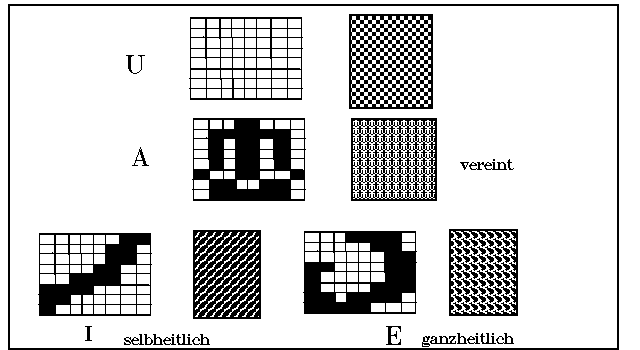
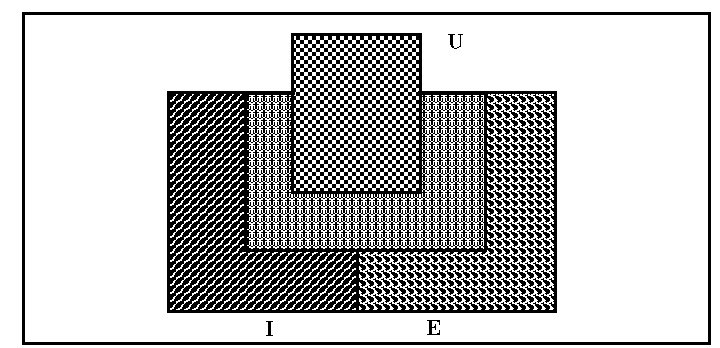
In All.3 sind die Muster harmonisch gegliedert. In All.3.1 sind die „Charaktere“
der Muster sichtbar. J ist „selbstheitlich“, E “ ganzheitlich“, A vereinigt die
Ge­gensätze der beiden. U schließlich ist „neutral“ und hat „Ähnlichkeit“
mit dem Muster beim magischen Quadrat 8×8, wenn man die ungeraden oder geraden Zahlen s oder w be­zeichnet. (ALLGLIED.PCX,
MU­STERA.PCX)

5. Ein Bilderkosmos vom Einfachen zum
Komple­xen

Grafikprogramme können bekanntlich patterns, wie sie nach 4.1 erstellt wer­den, benutzen, um begrenzte Felder damit zu füllen, aber auch um mit diesem pattern
selbst Linien zu zeichnen. In dem folgenden Bildern werden solche
patterns in Paintbrush (8 x 8) in beiden Funktionen benutzt. Die Bilder
ge­hen, so wie wir es in den Untersuchungen des Raumes zeigten, vom
Unendlichen ins Endli­che. Aus Platz­gründen können nur wenige Bilder
beigeschlossen werden. Be­reits in diesem relativ beschränkten
Grafikprogramm kann eine Vielzahl von Kon­zepten und Formen der bisherigen
Kunst­entwicklung integriert in einen neuen Gesamtzusammenhang ge­bracht
werden. Mit Farbe sind die Möglichkei­ten unver­gleichlich größer und
schließ­lich ist zu bedenken, dass diese Bilder di­gital
reprodu­ziert auf großen Monitor–Wänden
aus­gestellt werden sollten, um voll wirken zu können.
Selbstver­ständlich können solche Bilder zu Videofilmen usw. über
pi­xelweise Mutationspro­gramme fortgesetzt werden, womit die
Zeit­dimension hinzu­tritt. Weitere Möglichkeiten liegen in Verfahren
wie „Cyber-Space“.

Die folgende deduktive Bilderserie wird zuerst als Animation mit 4 Sekunden pro Bild abgespielt. Im folgenden sind die einzelnen Bilder auch einzeln
aufgeführt.

Animation

Einzelbilder

OR-OM0.PCX

OR-OM1.PCX

OR-OM2.PCX

OR-OM7.PCX

OR-OM12.PCX

OR-OM24.PCX

OR-OM27.PCX

OR-OM30.PCX

OR-OM34.PCX

OR-OM35.PCX

OR-OM53.PCX

OR-OM541.PCX

OR-OM65.PCX

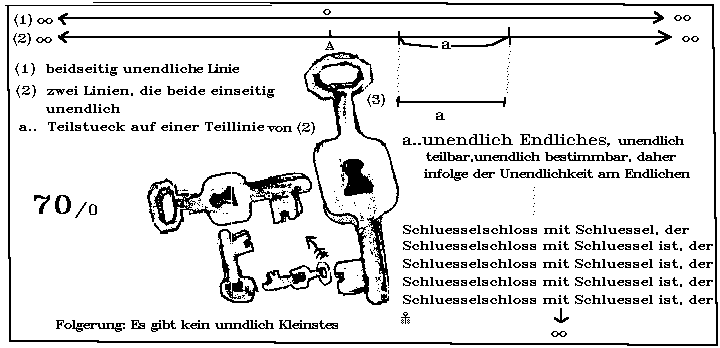
OR-OM70.PCX

OR-OM78.PCX

OR-OM80.PCX

OR-OM81.PCX

OR-OM891.PCX

OR-OM106.PCX

OR-OM107.PCX

OR-OM108.PCX

OR-OM85.PCX

OR-OM121.PCX

OR-OM122.PCX

OR-OM123.PCX

OR-OM130.PCX

OR-OM131.PCX

OR-OM133.PCX

OR-OM134.PCX

OR-OM135.PCX

OR-OM136.PCX

OR-OM137.PCX

OR-OM138.PCX

OR-OM140.PCX

OR-OM142.PCX

OR-OM143.PCX

OR-OM145.PCX

OR-OM146.PCX

OR-OM147.PCX

OR-OM148.PCX

OR-OM149.PCX